Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 4212345678910111213141516171819202122232425262728293031323334353637383940414344454647484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

Mudança de variável

Considere a integral

T = ∬ D x + y d x d y

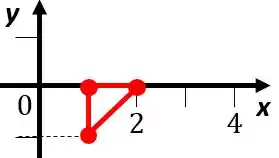
Onde D é o triangulo de vértices nos pontos 1,0 , 2,0 e 1 , - 1

  1. Usando a mudança de variáveis T u , v = x , y com u = x + y e v = x - y , encontre a região D * tal que T D * = D e esboce D e D *
  2. Determine a matriz jacobiana D T u , v .
  3. Mostre que T é injetora
  4. Calcule a integral dada usando a fórmula de mudança de variáveis

Passo 1

a )

A primeira coisa a fazer aqui é descobrir x e y em função de u e v . Agora já era né? Como vamos fazer isso? Imagina que u e v são constantes do sistema

x + y = u x - y = v

Somando as duas equações

2 x = u + v

x = u + v 2

Vamos agora substituir isso em uma das equações, eu vou colocar na primeira

u + v 2 + y = u

y = u - u + v 2

y = 2 u - u - v 2

y = u - v 2

A transformada vai ser

T u , v = u + v 2 , u - v 2

Essa leva os pontos em u , v para x , y

Podemos entender como a inversa dessa transformação como

T - 1 x , y = x + y , x - y

Essa é a transformada que leva os pontos x , y para u , v .

Passo 2

Ele quer a região D * , ou seja, os pontos u e v equivalentes aqueles que temos, então vamos transformar x e y em u e v para isso usamos T - 1 x , y em todos os pontos

T - 1 1,0 = 1 + 0,1 - 0 = 1,1

T - 1 2,0 = 2 + 0,2 - 0 = 2,2

T - 1 1 , - 1 = 1 + - 1 , 1 - - 1 = 0,2

Vamos ver como fica o gráfico de D

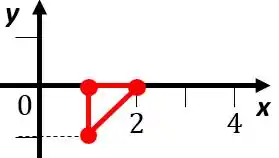
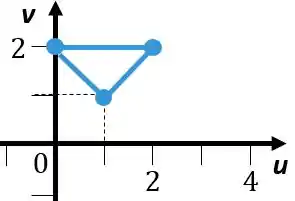
Agora o gráfico de D *

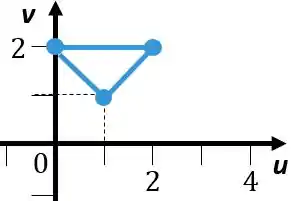
Passo 3

b )

Lembrando que, em T u , v , vamos ter

x = u + v 2

y = u - v 2

A matriz jacobiana vai ser

D T u , v = ∂ ( x , y ) ∂ ( u , v )     = ∂ x ∂ u u , v ∂ x ∂ v u , v ∂ y ∂ u u , v ∂ y ∂ v u , v

∂ x ∂ u = 1 2

∂ x ∂ v = 1 2

∂ y ∂ u = 1 2

∂ y ∂ v = - 1 2

D T u , v = 1 2 1 2 1 2 - 1 2

Passo 4

c )

Vamos ver se essa transformação é injetora, mas o que significa ser injetora? Temos que ver que se temos dois pontos iguais na transformação, eles são iguais em u e v .

Vamos pegar dois pontos

A = u 1 , v 1

B = u 2 , v 2

A transformação deles dois é igual, ou seja

T u 1 , v 1 = T u 2 , v 2

A transformação de A vai ser

T u 1 , v 1 = u 1 + v 1 2 , u 1 - v 1 2

A transformação de B vai ser

T u 2 , v 2 = u 2 + v 2 2 , u 2 - v 2 2

Se elas são iguais temos

u 1 + v 1 2 , u 1 - v 1 2 = u 2 + v 2 2 , u 2 - v 2 2

Isso nos diz que

u 1 + v 1 2 = u 2 + v 2 2

u 1 - v 1 2 = u 2 - v 2 2

Somando as duas equações vamos ter

2 u 1 2 = 2 u 2 2

u 1 = u 2

Substituindo isso na primeira equação

u 1 + v 1 2 = u 1 + v 2 2

v 1 2 = v 2 2

v 1 = v 2

Então no fundo temos que os pontos A e B são os mesmo, isso mostra que a função é injetora

Passo 5

d )

Antes de calcular a integral temos que calcular seu jacobiano

J = 1 2 1 2 1 2 - 1 2 = 1 2 - 1 2 - 1 2 1 2 = - 1 4 - 1 4 = - 1 2

Como o jacobiano não importa o sinal, vamos ter

J = 1 2

A integral vai ficar

T = ∬ D x + y d x d y = ∬ D * u + v 2 + u - v 2 1 2 d u d v = ∬ D * u 2 d u d v

Vamos ver agora o intervalo de integração, para isso vamos ver de novo o gráfico

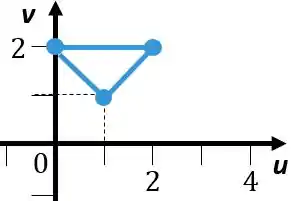
Aqui é mais fácil fazer a região do tipo II,

Temos que v vai de 1 à 2 , enquanto u vai de uma reta até a outra, precisamos achar a equação dessas retas., vamos começar pela reta mais a esquerda

v - 1 u - 1 = 2 - 1 0 - 1

v - 1 u - 1 = - 1

v - 1 = - u + 1

u = - v + 2

Vamos ver agora a reta pela direita.

v - 1 u - 1 = 2 - 1 2 - 1

v - 1 u - 1 = 1

v - 1 = u - 1

u = v

Agora podemos perceber que u vai de 2 - v até v

T = ∬ D * u 2 d u d v = ∫ 1 2 ∫ 2 - v v u 2 d u d v = ∫ 1 2 u 2 4 u = 2 - v v d v = ∫ 1 2 v 2 4 - 2 - v 2 4 d v

⇒ ∫ 1 2 v 2 4 - 4 - 4 v + v 2 4 d v = ∫ 1 2 v 2 4 - 4 4 + 4 v 4 - v 2 4 d v = ∫ 1 2 v - 1 d v

⇒ ∫ 1 2 v - 1 d v = v 2 2 - v v = 1 2 = 2 2 2 - 2 - 1 2 2 - 1 = 2 - 2 - 1 2 - 1

⇒ 0 - - 1 2 = 1 2

T = 1 2

Resposta

  1. R e g i ã o   D

    2. D * = t r i â n g u l o   d e   v é r t i c e s   2,0 , 2,2 , 1,1

  2. D T u , v = 1 2 1 2 1 2 - 1 2
  1. T = 1 2

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .