. Seja o paralelogramo com vértices , , e . Usando a mudança de variável e , calcule a integral.
Passo 1
Vamos começar essa questão descobrindo quem é e em função de e , ou seja:
Substituindo na outra equação e isolando o temos:
Além disso precisamos dos limites de integração e ficará muito mais fácil se olharmos para esse paralelogramo:
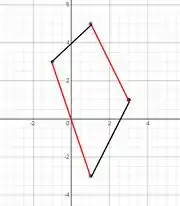
As retas pretas são dadas por
Olhando para os pontos que pertencem a cada reta podemos encontrar os limites de integração escolhendo um segmento e substituindo os pontos.
Para :
Para :
Com essas informações só nos falta calcular e montar a integral. Então, vem comigo!
Passo 2
Vamos calcular
Então pelo teorema de mudança de variável temos que:
E é esse o nosso resultado!