Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 3612345678910111213141516171819202122232425262728293031323334353738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

Questão 3: Seja a região D = x ,   y ∈ R 2   | e x 4 ≤ y ≤ e x ,   e - x ≤ y ≤ 4 e - x e considere uma mudança de variáveis T u ,   v = x u ,   v ,   y u ,   v de R 2 em R 2 que satisfaça às equações

u = e x v = y e x

Seja B a região do plano R 2 com coordenadas u , v tal que T B = D .

  1. Esboce as regiões D e B . Assinalem em seus esboços da região B pontos p 1 , p 2 , p 3 e p 4 na fronteira das curvas que limitam a região e, no esboço da região D , assinale suas imagens correspondentes T p 1 , T p 2 , T p 3 e T p 4 . Não é necessário calcular explicitamente as coordenadas dos pontos, embora possa ser desejável para verificar as contas.
  2. Escreva uma fórmula para T u ,   v , calcule a matriz Jacobiana D T e seu determinante.
  3. Use a mudança de variáveis T para calcular

∬ D   y 2 e 5 x   d x d y

Passo 1

Letra A)

Para desenhar a região D , primeiro, devemos tirar informações da própria definição de região:

D = x ,   y ∈ R 2   | e x 4 ≤ y ≤ e x ,   e - x ≤ y ≤ 4 e - x         →

y = e x 4           e         y = e x

y = e - x           e               y = 4 e - x

Ora! As duas primeiras são exponenciais:

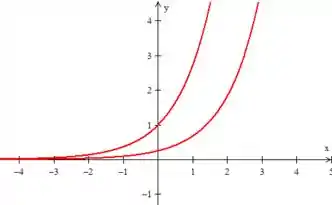
As duas últimas são exponenciais também, mas como temo - x como expoentes, as curvas devem estar refletidas em relação ao eixo x :

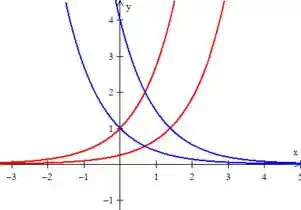
Então essa é a região:

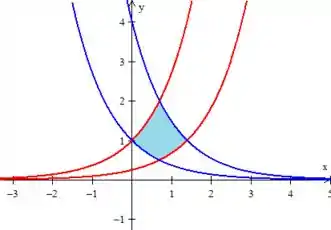
Passo 2

Para desenhar a região B , devemos desenhar as bordas obedecendo à definição:

u = e x v = y e x

Então as curvas que delimitam a região D ali em cima ficam sendo...

y = e x 4           e         y = e x                           →                               y = u 4           e         y = u

y = e - x           e               y = 4 e - x                             →                             y = 1 u             e             y = 4 u

Como y = v e x = v u ...    

      v u = u 4           e       v u = u v u = 1 u             e           v u = 4 u               →         v = u 2 4         e         v = u 2   v = 1           e           v = 4

Então essa daí é a equivalência da borda nesse munda de variáveis e é à borda da região D ! Basta desenhar isso então lembrando que no plano v u as duas equações de cima é uma parábola enquanto que as duas últimas são retas !

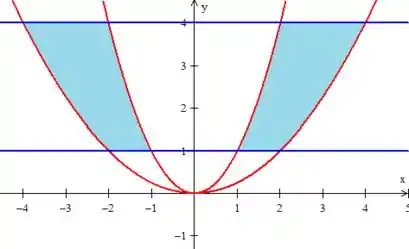
Passo 3

Assinalando os pontos no desenho como vimos é:

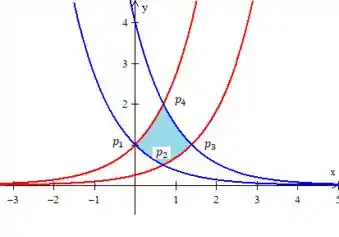
E no desenho da mudança...

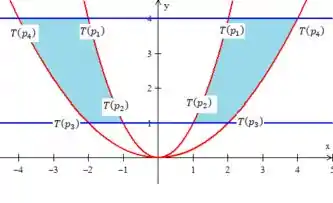
Passo 4

Letra B)

Sabemos que...

T u ,   v = x u ,   v ,   y u ,   v

Então temos que encontrar x em função de u e v e o mesmo para isso. Vamos fazer isso tentando isolá-las através da mudança...

u = e x v = y e x           →

Aplicando l n ...

ln ⁡ u = ln ⁡ e x v e x = y           →           ln ⁡ u = x v u = y    

Então...

T u ,   v = ln ⁡ u ,   v u

Passo 5

Para calcular o Jacobiano, podemos fazer...

J = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

Como

ln ⁡ u = x v u = y

Então...

J = 1 u 0 - v u 2 1 u = 1 u 2

Passo 6

Letra C)

Agora vamos calcular a integral...

∬ D   y 2 e 5 x   d x d y

Bem, então a mudança que vamos fazer basicamente é essa:

ln ⁡ u = x v u = y

Lembrando que o Jacobiano é:

J = 1 u 0 - v u 2 1 u = 1 u 2

Passo 7

Substituindo tudo então na integral dupla para u v ...

∬ D   y 2 e 5 x   d x d y = ∬ B   v u 2 e 5 ln ⁡ u ⋅ J   d u d v =

∬ B   v 2 u 2 u 5 ⋅ 1 u 2   d u d v = ∬ B   u v 2   d u d v

Veja que mudamos a região de D para B , já que estamos falando agora de uma integral dupla nas variáveis novas! Para calcularmos a integral então, deveríamos descrever a região e integrarmos, mas como a região nossa é simétrica em relação à ao eixo v :

E, além disso, se observarmos que estamos integrando uma função que que assume os mesmos valores dos dois lados do plano, mas com sinais diferentes:

- u v 2 = - u v 2

Se calcularmos essa integral então:

∬ B   u v 2   d u d v

Só pode dar 0 , já que a estamos somando os mesmos valores de um lado e o mesmo do outro só que com valor negativo!

∬ B   u v 2   d u d v = 0

Resposta

Letra A)

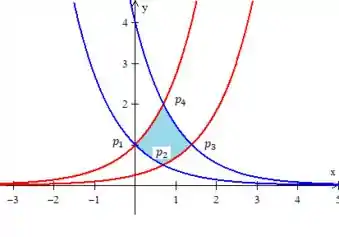
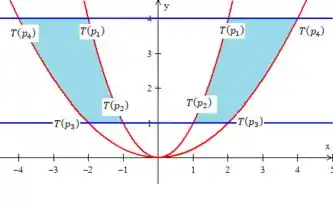
Letra B)

T u ,   v = ln ⁡ u ,   v u

J = 1 u 0 - v u 2 1 u = 1 u 2

Letra C)

∬ B   u v 2   d u d v = 0

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .