Um cilindro homogêneo de massa e raio sobe um plano inclinado de um ângulo em relação à horizontal sob a ação de uma força constante, como mostra a figura abaixo. O cilindro parte do repouso e sua velocidade angular aumenta com o tempo. Sabe-se que o cilindro rola sem deslizar e que seu momento de inércia em relação a um eixo perpendicular que passa pelo seu centro de massa é .
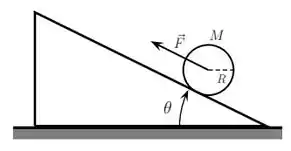
a) No rolamento sem deslizamento de um corpo rígido de raio , a relação entre os módulos da aceleração do centro de massa de um corpo rígido e a aceleração angular do corpo em relação ao centro de massa é . Justifique essa relação.
Passo 1
Na letra (a), queremos mostrar aquela relação de rolamento sem deslizamento:
De onde vem isso?
Primeiro de tudo, um rolamento é a soma de um movimento de translação com um movimento de rotação.
Movimento de translação:
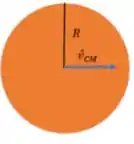
No movimento de translação, todos os pontos apresentam uma velocidade igual à velocidade do centro de massa:
Movimento de rotação:
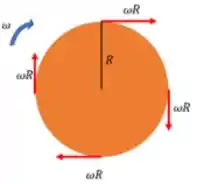
Enquanto no movimento de rotação, todos os pontos apresentam uma velocidade dada pela velocidade angular do corpo vezes sua distância ao eixo de rotação :
Passo 2
Ah, até aí okay... mas como eu mostro aquela relação?
Aí que está a sacada!
Rolamento (translação+rotação):
Para que não haja deslizamento, o ponto de contato com o chão deve estar parado, assim, suas velocidades translação e de rotação devem se cancelar:
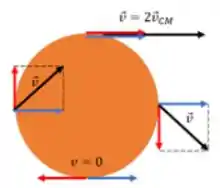
Então, apenas com essa relação entre e , o ponto de contato na extremidade não irá deslizar.
Por último, basta derivar essa expressão:
A derivada da velocidade é a aceleração , enquanto a derivada da velocidade angular é a aceleração angular :
Resposta
Ei, a resposta está no passo a passo :)