Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Rolamento sem Deslizamento

Ver Teoria
Exercício 281234567891011121314151617181920212223242526272930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Corpos Rígidos

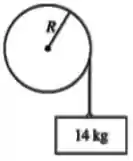
Uma corda ideal está enrolada em torno de um disco de raio R = 2,0   m . Ela pode desenrolar-se sem deslizar. O disco está montado num eixo sem atrito que passa pelo seu centro. Um bloco de massa m = 14   kg está preso à extremidade livre da corda, conforme mostra a figura. Quando o sistema é liberado a partir do repouso observa-se que o bloco desce 10   m em 2,0   s . Responder justificando:

Qual o momento de inércia do disco?

Passo 1

Vamos começar pensando no bloco? Ele faz um MUV, certo? Então podemos achar a aceleração do bloco aplicando a equação da posição para MUV.

S = S 0 + v 0 t + a t 2 2

10 = 0 + 0 + a 2 2 2

a = 5 m / s 2

Passo 2

Podemos calcular a tensão da corda aplicando a segunda lei de Newton para o bloco (adotando o sentido positivo para baixo)

m a = P - T

T = P - m a = m g - m a

T = m g - a

T = 14 9,8 - 5

T = 67,2 N

Passo 3

Podemos usar também a segunda lei de Newton para rotações no disco

I α = τ

Quem exerce torque no disco é a tensão T que é aplicada a uma distância R do eixo de rotação. Assim

I α = R T

Como a corda não desliza sobre o disco podemos usar a seguinte relação

α = a R

Assim

I a R = R T

Isolando o momento de inércia

I = R 2 T a

Agora é só jogar os valores!

I = 2 2 ⋅ 67,2 5  

I = 53,76   K g ⋅ m 2

Resposta

I = 53,76   K g ⋅ m 2

Exercícios de Livros Relacionados

Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na Fig. 11-60, uma força horizontal constante F → de módulo 12N é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é 10k g , o raio é 0,
10.3E Um cilindro rola em uma rampa de inclinação θ = 30 ° . A) Calcule a aceleração angular do cilindro B) Calcule a força de atrito da rampa sobre o cilindro.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida