Dois objetos A e B, ambos de seção circular de mesmo raio, rolam sem deslizar ao longo de umasuperfície inclinada, acelerando a medida que descem. Se o objeto A chega antes que o objeto B na base da superfície, é possível afirmar com certeza:

1. a massa de A é maior que a de B.
2. a massa de A é menor que a de B
3. o momento de inércia de A é maior que o de B.
4. o momento de inércia de A é menor que o de B
5. Nenhuma das anteriores.

Dado: Momento de inércia de uma esfera de massa e raio cujo eixo de rotação passa pelo centro de massa da esfera:

Bom, as forças que agem sobre a esfera no topo do plano são:

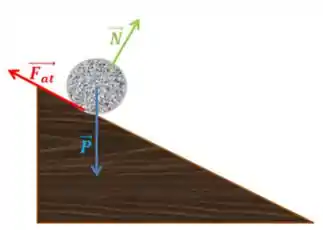
Beleza? Bom, vamos usar a segunda lei de newton pra calcular a aceleração da esfera.

Vamos usar a direção do plano e decompor a força peso naquela direção.

A força peso naquela direção vale:

Nessa direção, a força de atrito se opõem à direção do movimento:

Essa é a nossa primeira equação.

A segunda equação diz respeito à rotação da esfera. Bom, a força que executa um torque nessa esfera é a força de atrito. Assim, usando a segunda lei de Newton pra rotações:

E como a esfera rola sem deslizar( estamos supondo) então:

Assim, temos as três equações:

Isolando na terceira equação e substituindo na segunda:

Agora que sabemos uma expressão pra força de atrito, vamos substituir na primeira equação:

Beleza? Então chegamos a uma conclusão. A aceleração de uma esfera que rola num plano inclinado é dada por:

Como você pode ver, a aceleração não depende:

1. Da massa.
2. Do momento de inércia.
3. Do raio.

E ai? Então, olhando pras opções, você pode chegar a alguma daquelas conclusões?

A resposta é: Não!

Mas por que uma esfera chegou na frente da outra? Bom, não temos informações suficientes pra saber, mas talvez elas sejam feitas de materiais diferentes, isso talvez causa diferentes forças de atrito, o que geraria acelerações finais diferentes.

Mas de qualquer forma, a resposta pra essa questão é:

e)