A figura ,que se refere às Questões 1, 2 e 3, representa um aro que rola sem deslizar sobre uma superfície horizontal.
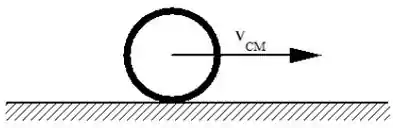
Suponha que a massa do aro seja e a velocidade do centro de massa seja . Dado que , onde é o raio do aro, a energia cinética do aro é
(A) J
(B) J
(C) J
(D) J
(E) J
Passo 1
A energia cinética total do aro será:
Já temos todos os dados, exceto a velocidade angular .
Passo 2
Como o aro rola sem deslizar, necessariamente temos que:
Então:
Passo 3
A energia cinética total será:
J
Ficamos com a letra (C).
Resposta
Letra (C)
Exercícios de Livros Relacionados
Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na Fig. 11-60, uma força horizontal constante F → de módulo 12N é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é 10k g , o raio é 0,
10.3E Um cilindro rola em uma rampa de inclinação θ = 30 ° . A) Calcule a aceleração angular do cilindro B) Calcule a força de atrito da rampa sobre o cilindro.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida