Um caixote é transportado numa plataforma horizontal apoiada sobre cilindros de raio . A plataforma se move para a direita com velocidade sem deslizar sobre os cilindros que rolam sem deslizar sobre a superfície horizontal. O módulo da velocidade angular de cada cilindro em relação ao seu centro de massa é
a)
b)
c)
d)
e)
Passo 1
Para resolver esse problema, devemos pensar em algum ponto que está em repouso no sistema. Este ponto é, em qualquer problema, o “Centro Instantâneo de Rotação”. Este ponto está no contato entre a roda e o solo, e ele está em repouso porque o rolamento é sem deslizamento. Portanto, temos:
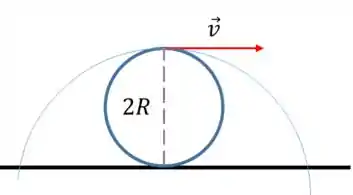
Como a velocidade angular é a mesma para qualquer ponto da roda, e como o centro instantâneo faz parte da roda, temos:
E então:
Resposta
(b)
Exercícios de Livros Relacionados
Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na Fig. 11-60, uma força horizontal constante F → de módulo 12N é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é 10k g , o raio é 0,
10.3E Um cilindro rola em uma rampa de inclinação θ = 30 ° . A) Calcule a aceleração angular do cilindro B) Calcule a força de atrito da rampa sobre o cilindro.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida