A figura ,que se refere às Questões 1, 2 e 3, representa um aro que rola sem deslizar sobre uma superfície horizontal.
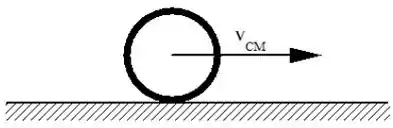
O ponto com maior rapidez em relação à superfície é
(A) o ponto de contato do aro com a superfície.
(B) o ponto no centro do aro.
(C) o ponto no topo do aro, oposto ao ponto de contato com a superfície.
(D) o ponto mais à frente do aro, na altura do seu centro de massa.
(E) o ponto mais atrás do aro, na altura do seu centro de massa.
Passo 1
A velocidade de um ponto do corpo é a soma da velocidade de translação do centro de massa com a velocidade resultante da rotação do corpo :
Mas como assim?
Bom, o corpo está transladando e rotacionando ao mesmo tempo.
Então, o movimento de cada ponto do corpo é a junção de cada um desses movimentos.
Se liga... se um corpo está em translação, todos os pontos desse corpo apresentam uma velocidade de translação igual a velocidade do centro de massa :
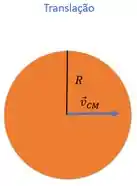
E se o corpo está em rotação, cada ponto do corpo apresenta uma velocidade linear resultante dessa rotação.
E essa velocidade é dada por:
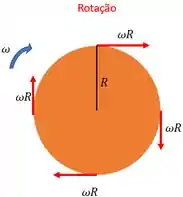
Beleza, mas num rolamento temos os dois movimentos acontecendo juntos, né?
Então, a velocidade de cada ponto vai ser a soma da velocidade de translação com a de rotação:
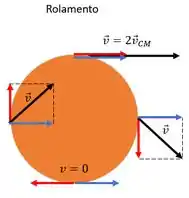
Mas podemos ver na figura que o ponto de maior velocidade será no topo do aro, pois tanto a velocidade de translação quanto a resultante da rotação apontam para o mesmo sentido.
Ficamos com a alternativa (C).
OBS: Especificamente no rolamento sem deslizamento, essa a velocidade do topo será o dobro da velocidade do centro de massa.
Isso porque a condição desse rolamento é que o ponto de contato esteja com velocidade zero (não deslize).
Assim, temos que:
Ou seja:
Resposta
Letra (C)