Seja um cilindro maciço e homogêneo, de raio e massa , (cilindro 1) que pode girar sem atrito em torno de um eixo vertical que passa pelo seu centro. O eixo está fixado em uma mesa horizontal, sobre a qual se encontra o cilindro. Enrolada na superfície curva do cilindro há uma corda inextensível, que passa por uma roldana e tem na extremidade livre um outro cilindro (cilindro 2) de massa que cai sob a ação da gravidade. As massas da roldana e da corda são desprezíveis e a corda não desliza.
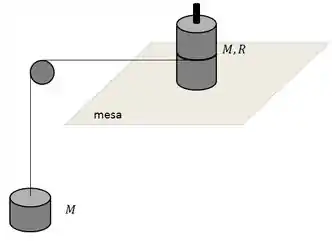
a) Nestas condições, escreva as equações de movimento do cilindro 1 e do cilindro 2
(isto é, escreva as equações que relacionam as forças existentes com as acelerações) e
calcule a tensão na corda.
Passo 1
(a)
O que tá acontecendo com os cilindros:
O 1 tá só rodando ali na mesa. Então a equação de movimento dele é aquela de rotação:
O 2 tá só caindo. Ele não gira. Então a equação de movimento dele é a segunda lei de Newton:
Passo 2
Então vamos começar com o cilindro 1:
A distância entre o eixo e o ponto de aplicação da força (Tração) que faz o cilindro girar é o próprio raio do cilindro. E o ângulo entre os vetores e é :
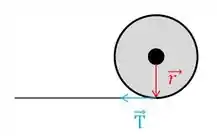
Então o módulo do torque é:
Agora, usando a relação entre o torque e a aceleração angular
Show! Essa é a nossa equação de movimento para o cilindro 1.
Agora vamos para o cilindro 2:
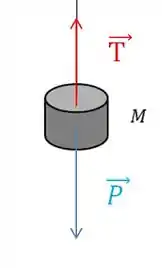
Como o cilindro tá descendo:
Beleza. Já temos as duas equações de movimento, uma para i cilindro 1 e outra para o cilindro 2.
Agora, vamos calcular a tensão na corda.
Passo 3
As equações de movimento são essas aqui:
Usando aquela relação da cinemática angular e que o momento de inércia de um cilindro que gira em torno de um eixo que passa pelo centro de massa é , podemos reescrever a primeira equação:
Isolando o :
Beleza, sabemos a aceleração, vamos substituir ela na outra equação de movimento pra acha a tensão, que é o que ele pede:
Arrumando isso e isolando o T:
Prontinho!!
Sucesso?
Resposta
(a)