Uma esfera de bronze sólida de massa e raio rola sem deslizar ao longo de um plano inclinado após ser solta do repouso de uma altura . O momento de inércia da esfera em relação a um eixo que passa pelo seu centro que centro é e a aceleração da gravidade é . O plano inclinado forma um ângulo com a horizontal, como mostra a figura abaixo:

(a) Há atrito entre a esfera e o plano inclinado? Como você chegou a essa conclusão?

(b) Há conservação de energia mecânica? Justifique sua resposta levando em consideração o respondido no item (a).

(c) Utilizando considerações de energia, determine a velocidade com que a esfera atinge a base do plano inclinado.

(d) Obtenha a velocidade na base do plano inclinado já calculada no item (c) utilizando agora considerações de dinâmica (ou seja, aplicando a segunda lei de Newton).

(b)

Sim! Há conservação da energia mecânica.

Eita, mas a gente acabou de ver que tem atrito estático. Esse atrito não era para estar roubando energia do nosso sistema? Então, muita calma nessa hora. A energia que a roubaria do sistema é igual ao trabalho dela:

Mas nós vimos também que o ponto de contato entre a esfera e o plano está em repouso, ou seja o deslocamento é zero! Logo

Assim a energia mecânica se conserva!

(c)

Com falamos na letra (b), a energia mecânica se conserva, então:

No início, ele sai do repouso lá da altura . Quando ele chega lá embaixo, a altura é 0 e só temos energia cinética, beleza? Lembrando que é um rolamento sem deslizamento, então temos uma energia cinética de rotação também:

Podemos usar o vínculo

Então:

Lá no enunciado ele fala pra gente o momento de inércia, então vamos substituir:

Resolvendo isso daí:

Show??!

(d)

Temos que obter a mesma velocidade, mas agora usando leis de Newton.

Então vamos começar fazendo o diagrama de corpo livre:

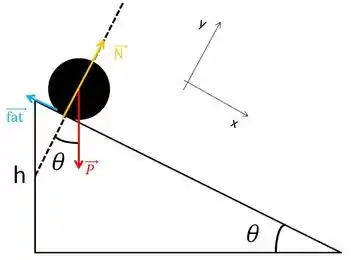
Já coloquei o ângulo ali na posição e também já mostrei o eixo de coordenadas que vamos utilizar.

Decompondo as nossas forças:

Então aplicando a segunda lei de newton.

No eixo x:

Daqui podemos dizer que:

No eixo y, a aceleração é zero, já que não há movimento nesse eixo:

Beleza, essas foram as equações de movimento para a translação do centro de massa.

Mas a esfera também está rodando, então, vamos equação de movimento para rotação:

Como se trata de um rolamento sem deslizamento, podemos usar:

Então:

A força responsável pela rotação é a , e ela produz um torque cujo módulo é igual a:

Então:

Agora vamos voltar lá na equação de translação do centro de massa:

Podemos igualar essas duas equações de pra achar a aceleração:

Resolvendo:

Beleza! Acabou? Não!!!

Porque a gente quer a velocidade com que a esfera chega lá embaixo. Então, por torriceli:

Ele sai do repouso, então

Para achar o

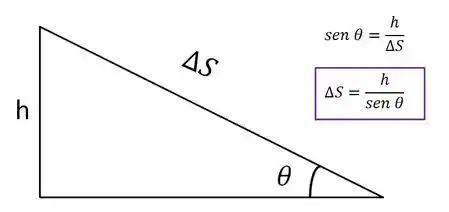
Beleza, substituindo:

Então:

Igual ao da letra (c)!