Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Rolamento sem Deslizamento

Ver Teoria
Exercício 611234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Um corpo homogêneo, de seção reta circular de raio R = 0,4   m , é liberado do repouso e rola sem deslizar sobre um plano inclinado. O gráfico da velocidade do centro de massa do corpo v em função do tempo t é mostrado na Figura 2

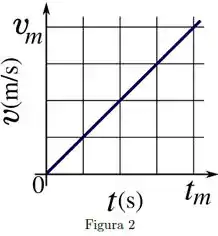
onde t m = 3,0   s e v m = 12   m / s . Qual é a aceleração angular do corpo?

(a) 0   r a d / s 2

(b) 5   r a d / s 2

(c) 10   r a d / s 2

(d) 15   r a d / s 2

(e) 25   r a d / s 2

(f) 35   r a d / s 2

Passo 1

Nosso objetivo é achar a aceleração angular do corpo α .

Mas como o corpo rola sem deslizar, podemos relacionar α com a aceleração do centro de massa a :

a = α R

Ah beleza, mas como achamos a aceleração do centro de massa a ??

Isso mesmo, com a única outra informação que temos... o gráfico.

Passo 2

Temos um gráfico da velocidade v do centro de massa em função do tempo t do centro de massa.

Podemos calcular a aceleração com:

a = ∆ v ∆ t

No gráfico isso fica:

a = ∆ v ∆ t = v m - 0 t m - 0

a = v m t m = 12 3

a = 4   m / s 2

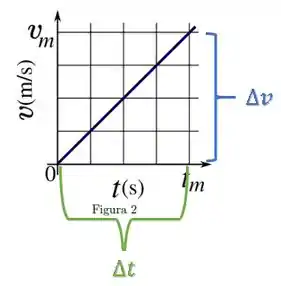
OBS: Isso é o mesmo que calcular a inclinação da reta (tangente do ângulo de inclinação).

Passo 3

Agora que temos a aceleração do centro de massa, basta achar a aceleração angular:

a = α R

α = a R

α = 4 0,4

α = 10   r a d / s 2

Ficamos com a alternativa (c).

Resposta

Letra (c)

Exercícios de Livros Relacionados

Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na Fig. 11-60, uma força horizontal constante F → de módulo 12N é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é 10k g , o raio é 0,
10.3E Um cilindro rola em uma rampa de inclinação θ = 30 ° . A) Calcule a aceleração angular do cilindro B) Calcule a força de atrito da rampa sobre o cilindro.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida