Três objetos são liberados do repouso e rolam sem deslizar sobre um plano inclinado, que faz um ângulo com a horizontal. Os três objetos possuem a mesma massa e raio , e possuem respectivamente momentos de inércia , e e acelerações , , e . O que se pode afirmar sobre os módulos das acelerações?
(a)
(b)
(c)
(d)
(e)
(f)
(g) Não é possível determinar
Passo 1
Já que em todos os casos não há deslizamento, todos eles precisam entrar em rotação para que descam o plano inclinado.
Assim, a ideia é que quanto maior o momento de inércia do corpo, mais dificuldade a entrar em rotação ele apresenta...
Portanto, o corpo que apresenta momento de inércia é o corpo com maior resistência a entrar em rotação e por isso apresenta a menor aceleração para descer a rampa.
Ele vem seguido do corpo com e por último . Logo:
Ficamos com a letra (a). Mas vamos fazer umas continhas para a gente confirmar essa ideia.
Passo 2
Primeiro vamos dar uma olhada no diagrama de forças sobre o corpo:
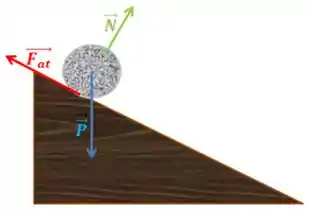
OBS: Lembrando que deve existir uma para que o corpo desca sem deslizar.
A segunda Lei de Newton na direção da rampa é:
Enquanto a segunda Lei de Newton para rotação é:
Os torques das forças peso e normal são nulos pois a primeira está aplicada no centro de rotação do corpo e a segunda é paralela à direção do vetor posição .
Resta apenas o torque da força de atrito que está perpendicular ao vetor posição :
Passo 3
Ficamos com essas duas equações:
Como é um rolamento sem deslizamento, podemos usar a relação:
Queremos a aceleração , então vamos utilizar a expressão na segunda equação para subsituir :
Ficamos com
Podemos substituir a da segunda equação na primeira.
Na segunda equação, temos:
Substituindo isso na primeira:
Pronto, chegamos numa expressão para a aceleração.
Passo 4
Repara que quanto maior for o momento de inércia , maior será o denominador da fração. Ou seja, menor será a aceleração .
O que confirma nossa ideia inicial:
Resposta
Letra (a)