Uma roda de massa , raio e momento de inércia em relação ao seu eixo de simetria, tem seu eixo ligado a uma mola ideal de constante , preso a uma parede. A roda gira sem deslizar sobre um piso com atrito estático . é a posição dp centro de massa com relação ao ponto de equilíbrio.
(a) Para um movimento para a direita (valores positivos de ), qual direção da aceleração do centro de massa? A direção da aceleração angular em relação ao centro de massa (horário ou anti-horário)? A direção do atrito estático, ? E a direção do torque, ?
(b) Encontre a força de atrito , em função de e .
(c) Encontr a força resultante em função de e .
Passo 1
Para um movimento para a direita (posição é positiva), a mola está esticada. Assim, temos que a força elástica está para a esquerda:
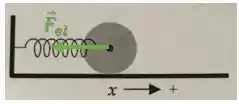
Isso acontece tanto se a roda estiver ainda andando para a direita e desacelerando quanto se ela já estiver retornando em direção ao ponto de equilíbrio acelerando.
Em ambos esses movimentos, a tendência de deslizamento da roda é para o sentido horário, portanto a força de atrito age contra essa tendência e tenta girar a roda no sentido anti-horário:
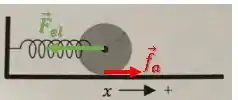
Esse sentido da força de atrito às vezes gera uma confusão...
Mas olha só, todas as forças atuando sobre o disco:
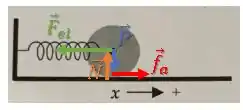
Tanto a força elástica quanto a força peso estão aplicada no próprio centro de massa, por isso não geram torque.
Já a força normal, também não gera torque pois está numa direção que passa pelo centro de massa.
Então, a ÚNCIA força que exerce TORQUE é a força de atrito .
O disco rola sem deslizar, ou seja, a força de atrito é a única responsável por alterar a rotação do disco.
Assim, quando o disco está andando para a direita com positivo sua translação e rotação são assim:
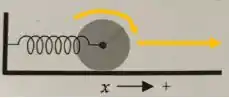
Mas a roda está desacelerando devido à força elástica.
E para isso a força de atua tentando diminnuir sua velocidade angular:
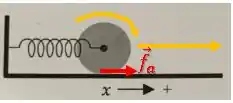
Então, agora vamos responder a letra (a).
Passo 2
(a) Para um movimento para a direita (valores positivos de ), qual direção da aceleração do centro de massa?
A aceleração está na direção da força resultante:
Se a força elástica aponta para a esquerda, sua aceleração será para a esquerda.
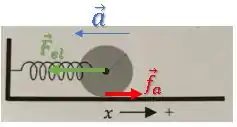
ainda que a força de atrito atue para a direita, ela é sempre menor que a força elástica:
A aceleração angular será no sentido anti-horário.
Consequência do torque da força de atrito , também nesse sentido.
Passo 3
Na letra (b), queremos a força de atrito .
Para isso vamos aplicar a segunda lei de Newton para translação e para rotação.
Passo 4
Aplicando a segunda lei de Newton para rotação, temos:
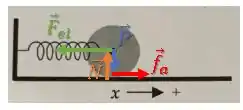
Vimos no PASSO 1 que apenas a força de atrito gera torque:
Como o rolamento acontece sem deslizamento, podemos relacionar a aceleração do centro de massa com a aceleração angular :
Substituindo isso, temos:
Além disso, o momento de inércia da roda foi dado:
Substituindo isso:
Cortando os raios :
Passo 5
Substituindo o valor da aceleração na segunda lei de Newton para translação, temos:
Passo 6
Na letra (c), queremos a força resultante .
Bom, nós calculamos isso na Segunda lei de Newton para translação:
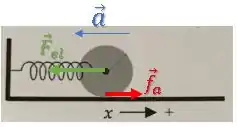
Mas, agora sabemos o valor de em função de e :
Resposta
(a)
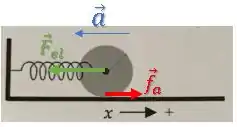
Aceleração do centro de massa para a esquerda.
Aceleração angular no sentido anti-horário.
Força de atrito para a direita.
Torque no sentido anti-horário.
(b)
(c)