Uma esfera desce um plano inclinado de um ângulo em relação à direção horizontal, rolando sem deslizar, sujeita à ação apenas das forças peso, normal e atrito. É correto afirmar que:
(a) Apenas a força de atrito exerce torque em relação ao centro de massa da esfera.
(b) Apenas a força peso exerce torque em relação ao centro de massa da esfera.
(c) As forças peso e atrito exercem trabalho diferente de zero sobre a esfera.
(d) A força normal não exerce torque em relação ao centro de massa pois atua no centro de massa da esfera.
(e) O centro de massa da esfera desce a rampa com aceleração constante igual a .
(f) Os trabalhos realizados pelas forças normal e de atrito se cancelam.
Passo 1
Olhando a situação de lado, temos as seguintes forças:
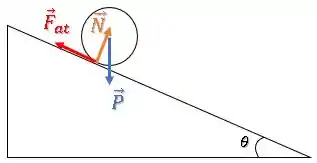
Passo 2
(a) Apenas a força de atrito exerce torque em relação ao centro de massa da esfera.
(b) Apenas a força peso exerce torque em relação ao centro de massa da esfera.
Vamos analisar os torques dessas forças.
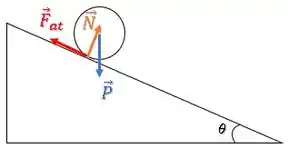
Como a força peso está aplicada no centro de rotação da esfera, ela não gera torque:
Já a força normal, não está aplicada no centro de rotação, porém ela está numa direção que passa em cima do centro de rotação da esfera. Logo, seu torque também é nulo:
A única que realiza torque realmente é a força de atrito, que está aplicada na extremidade da esfera e numa direção que não passa por cima do centro de rotação.
Inclusive, como essa força é tangencial à esfera, seu torque é:
Logo, a letra (a) é verdadeira, e a (b) falsa.
Já achamos nossa resposta mas vamos dar uma olhadinha nas outras.
Passo 3
(c) As forças peso e atrito exercem trabalho diferente de zero sobre a esfera.
(f) Os trabalhos realizados pelas forças normal e de atrito se cancelam.
Essas afirmativas são falsas, pois ambas as forças não exercem trabalho sobre a esfera.
Entretanto, seus trabalhos são nulos por razões diferentes.
O trabalho é dado pelo produto escalar entre a força e o deslocamento:
Força normal:
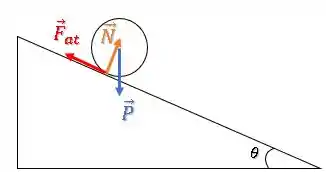
Como a força é perpendicular ao deslocamento, temos:
Ou seja, quando a força é perpendicular ao deslocamento ela não realiza trabalho.
Força de atrito:
Agora a questão é um pouco diferente.
Como não há deslizamento, o ponto de contato entre a esfera e o chão está sempre parado.
Logo, não há deslocamento no ponto de aplicação da força de atrito.
Por isso, o trabalho dessa força é nulo.
Passo 4
(d) A força normal não exerce torque em relação ao centro de massa pois atua no centro de massa da esfera.
Como vimos no PASSO 2, realmente a força normal não exerce torque sobre o centro de massa.
Porém, ela não está aplicada no centro de massa e sim no ponto de contato da esfera com o chão.
Afirmativa (d) está errada.
Passo 5
(e) O centro de massa da esfera desce a rampa com aceleração constante igual a .
Aplicando a segunda lei de Newton para translação na direção da rampa temos:
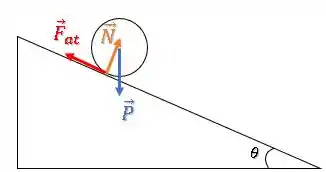
Temos a componente para baixo da rampa e a força de atrito para cima da rampa, logo:
Assim, a aceleração é diferente do que diz a afirmativa:
A afirmativa (e) também é falsa.
Ficamos com a letra (a).
Resposta
Letra (a)