Um carretel de raio externo, raio interno (), massa e momento de inércia em relação ao centro de massa é puxado ao longo de um piso horizontal rugoso por um fio que exerce uma tração , conforme a figura. O coeficiente é um número adimensional e o coeficiente de atrito estático é . Suponha haver rolamento sem deslizamento. Faça corretamente o que for solicitado em função dos dados fornecidos a partir das leis físicas sobre torque e rolamento.

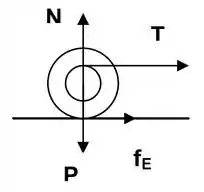
Obtenha uma expressão para o valor da aceleração do centro de massa .

Encontre uma expressão para o módulo da força de atrito estático

Agora considere que o carretel é jogado tangencialmente sobre o piso (cujo coeficiente de atrito cinético vale ) com velocidade inicial do centro de massa , no sentido positivo do eixo , e velocidade angular inicial . Não há tração nesse caso. Seja , e . Determine se no instante de tempo quando e o carretel parou de deslizar e iniciou o rolamento sem deslizamento.

Para o movimento rotacional, a Segunda Lei de Newton para rotações nos diz;

Para o sistema, temos em módulo(Adotando o sentido horário como positivo):

Como o corpo rola sem deslizar, podemos substituir por :

Agora que temos as duas equações, podemos eliminar a força de atrito, que não é dada!

Substituindo o momento de inércia e isolando a aceleração, temos:

Agora que já temos o valor a aceleração, só precisamos substituir na equação do movimento translacional:

No instante , ele nos diz que a velocidade do centro de massa , enquanto a velocidade angular . Quando não ocorre deslizamento, temos que , Para , temos:

Como temos :

Ou seja, o corpo não parou de deslizar!