Um cilindro maciço de massa e raio desce rolando sem deslizar sobre um plano inclinado de em relação à horizontal. O cilindro parte do repouso e percorre uma distância no plano inclinado. Qual é a velocidade de seu centro de massa no final da distância ? (Dado: .)

(A)

(B)

(C)

(D)

(E)

Inicialmente, a bola está em repouso. Assim, ela terá apenas energia potencial gravitacional :

Após a bola percorrer uma distância , ela estará com uma velocidade do centro de massa (translação) e também uma velocidade angular de rotação em torno do seu centro de massa. Por isso ela terá tanto energia cinética de translação quanto energia cinética de rotação :

Logo, podemos igualar a energia inicial com a final:

Até aí, okay...

Mas reparem que não sabemos nem .

Como achamos esses caras?

Começando com :

Inicialmente, o cilindro estava a uma altura vertical . Porém, sabemos o quanto ele andou na direção da rampa, então podemos relacionar os dois a partir da inclinação da rampa:

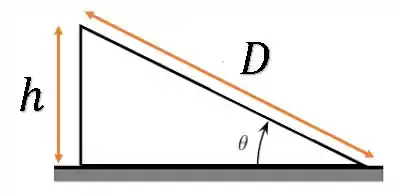
Como o ângulo de inclinação da rampa é , temos:

Relacionando :

A princípio parece que não temos nenhuma relação para , entretanto o enunciado diz que o cilindro desce rolando sem deslizar.

Assim, as velocidades do centro de massa e a velocidade angular se relacionam por:

Como queremos no final das contas a , vamos isolar e substituir :

Beleza, com essas duas relações, podemos encontrar o que queremos na expressão de energia:

Podemos ainda susbtituir a expressão para o momento de inércia do cilindro, dado por:

Então:

Cortando os :

Cortando as massas :

Substituindo os valores, temos:

Achamos então que a velocidade do centro de massa é:

Ficamos com a letra (D).