Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
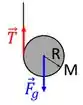
A figura abaixo mostra um ioiô na forma de um disco homogêneo de raio R e massa M. Quando o ioiô é liberado do repouso no instante t = 0, o fio ideal ao seu redor desenrola sem deslizar. O ioiô então executa um movimento vertical descendente com rotação ao redor do eixo perpendicular à sua superf ́ıcie e passando no seu centro de massa (CM).
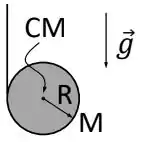
a) Desenhe o diagrama de corpo isolado do ioiô, identificando cada força e o seu ponto de aplicação.
B) Calcule a aceleração do CM do ioiô. Deixe sua resposta em função apenas da aceleração da gravidade g.
Dado: Momento de inércia de um disco homogêneo de raio R e massa M ao redor do eixo perpendicular a sua superfície e passando no seu CM:
C) Calcule a velocidade angular do ioiô no instante t. Deixe sua resposta em função apenas de t, R e g.
Passo 1
Temos a força gravitacional , atuando sobre o CM e • tração da corda , atuando na borda do ioiô.
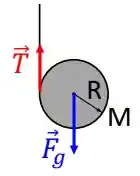
Passo 2
Segunda Lei de Newton para forças e torques. Ficamos com:
E nos torques:
Como , temos:
Subsituindo na primeira equação, temos:
Showw! Quase acabando!
Passo 3
A aceleração do centro de massa é constante e a aceleração angular α tá relacionada com a aceleração do CM a através de α = a/R. A velocidade angular então pode ser calculada por:
Como a velocidade angular inicial é nula, temos:
Conseguimosss!
