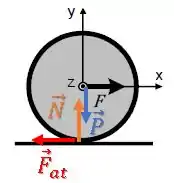
O disco mostrado na figura tem massa e raio e está sendo puxado por uma força horizontal aplicada em seu centro de massa. Ele rola sem deslizar sobre uma superfície horizontal áspera. O coeficiente de atrito estático entre o disco e a superfície é . Obtenha os resultados em função dos dados fornecidos.
a) Faça o diagrama de forças sobre o disco. Determine uma expressão literal para o módulo da aceleração angular 𝛼 do disco. Faça o mesmo para o módulo e o sentido da força de atrito .
Passo 1
Sobre o diagrama de forças...
Temos a força peso sobre o centro do disco para baixo, a força normal no ponto de contato para cima.
Como a bola tende a arrastar para a direita com a translação, a força de atrito está contra essa tendência de deslizamento e atua para a esquerda, fazendo a bola girar no sentido horário.
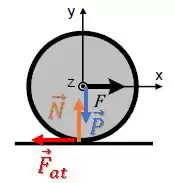
Passo 2
Agora, queremos a aceleração angular e a força de atrito .
Para encontrar isso, vamos escrever as duas equações de movimento do disco.
Translação:
Rotação:
E além disso, como o disco rola sem deslizar, sua aceleração do centro de massa e sua aceleração angular estão relacionados por:
Juntando essas três equações conseguimos resolver o problema.
Passo 3
Na equação de translação, temos:
Temos que tomar cuidado para NÃO substituir a força de atrito por:
Pois, essa é a expressão para a força de atrito estático máxima, mas não podemos garantir isso na questão (aquele dado é pegadinha).
Passo 4
Para a rotação, temos:
O torque resultante será a soma dos torques de cada uma das forças:
Vamos a cada um deles...
A força peso está aplicada no próprio centro de massa, então ele está a uma distância nula, por isso não gera torque:
Para a força normal, temos o vetor paralelo ao vetor :
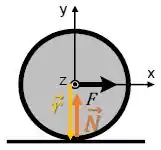
Logo, o torque dessa força também é nulo:
A força também está aplicada no centro do disco, então seu torque é nulo:
Já a força de atrito vai gerar um torque, seus vetores e são:
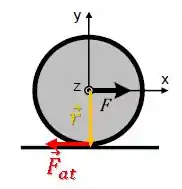
Como os vetores são perpendiculares, temos que o módulo do torque é:
Assim, vamos ter:
Passo 5
Juntando as nossas duas equações de movimento com a condição de rolamento sem deslizamento, temos esse sistema:
Queremos , então, vamos usar a relação de não deslizamento para retirar da primeira equação:
O momento de inércia de um disco é:
Substituindo esse valor na segunda equação, temos:
Então, nosso sistema ficou:
Somando as duas equações, temos:
Achamos que a aceleração angular é:
E conseguimos substituir esse valor na segunda equação para achar a força de atrito também:
A direção e o sentido já estão na figura, mas também podemos escrever a força de atrito apontando para o sentido negativo do eixo :
Resposta