Um cilindro rígido e homogêneo de massa e raio está sobre uma superfície horizontal e pode girar livremente em torno de seu eixo de simetria longitudinal, como indicado na figura. O eixo está preso a uma extremidade de um fio ideal que passa por uma polia ideal e tem em sua outra extremidade um bloco suspenso de massa . O bloco desce verticalmente com aceleração para baixo e o cilindro rola sem deslizar sobre a superfície horizontal devido ao seu atrito com ela. O momento de inércia do cilindro relativo ao eixo de simetria é . Considere como dados e o módulo da aceleração da gravidade.
a) Indique todas as forças externas que atuam sobre o bloco e sobre o cilindro.
b) Calcule o módulo da aceleração do bloco;
c) Calcule o módulo da força de atrito sobre o cilindro e indique o seu sentido.
Passo 1
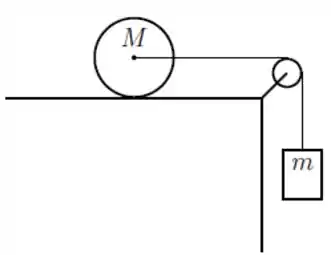
As forças atuando no cilindro são seu peso , a força normal da superfície , a tração do fio , e a força de atrito .
Tendo rotação, rolamento sem deslizar e tal é normal a gente ficar confuso pra que lado aponta a força de atrito. Nesse caso a gente faz o seguinte: “chuta” um lado e depois vê se vai dar certo! Se no fim o módulo der negativo, basta trocar o sentido! Então digamos que a força de atrito aponta pra esquerda.
Assim, o diagrama das forças atuando no cilindro é:
Passo 2
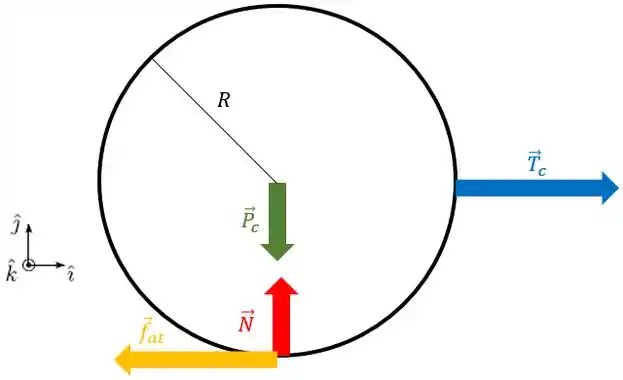
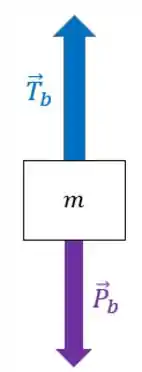
Vamos ver o bloco agora.
Nele só tem as forças peso e a tração do fio :
Passo 3
b)
Um aviso antes da gente mergulhar de cabeça nas contas: sempre que eu botar um vetor mas sem a flechinha em cima é porque é o módulo dele, beleza? Tipo é o módulo de .
Dito isso, vamos aplicar a 2ª lei de Newton pro bloco:
Como ele está descendo, em módulo vamos ter
Passo 4
Agora vamos pro cilindro! Temos que ficar ligados porque ele, além da translação, tem uma rotação.
Vamos começar aplicando a 2ª lei de Newton pra translação. Seja a aceleração do centro de massa do cilindro. Ela é toda pra direita, então no eixo temos:
Como o cilindro vai pra direita, em módulo temos
Obs: não vamos nos preocupar com as forças no eixo e porque elas não têm importância pra essa questão.
Passo 5
Beleza, agora vamos dar uma olhada na rotação.
As forças peso, normal e de tração estão na direção do centro do cilindro, que é onde fica o eixo de rotação. Então essas forças não realizam torque, somente a realiza.
O braço da alavanca é o próprio raio do cilindro, então o torque da força de atrito é dado por:
O sinal negativo é porque o torque produzido é no sentido horário, e o sentido anti-horário que é o considerado positivo.
Passo 6
Portanto, pela 2ª lei de Newton,
A aceleração é no sentido horário, então ela também é negativa:
Passo 7
Então vamos ter:
Os sinais de negativo vão cortar:
E em módulo:
Passo 8
Show! De todas essas equações, obtivemos o sistema:
Mas ainda dá pra ajeitar várias coisas aí!
Passo 9
Primeira observação: os fios e a polia são ideais, então as forças de tração e as acelerações nos blocos têm o mesmo módulo! Isto é,
Tem que ficar ligado nisso, quase toda questão desse tipo envolve isso!
Passo 10
Outra coisa é que o momento de inércia é , então podemos ajeitar a última equação do sistema:
Passo 11
E também temos a relação
Logo,
Passo 12
Beleza, então agora o nosso sistema ficou assim:
Passo 13
Vamos somar as 2 primeiras equações:
Passo 14
Agora vamos substituir a 3ª equação nessa que achamos, aí dá:
Passo 15
Vamos isolar o , que é o que a gente quer achar:
Passo 16
c)
Agora só falta calcular o módulo da força de atrito! Vimos que
Ou seja,
Todos os valores envolvidos são positivos, então . Isso confirma que lá no começo escolhemos o sentido certo pra força de atrito, ela aponta pra esquerda mesmo!
Resposta
a)
b)
c)