Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Rolamento sem Deslizamento

Ver Teoria
Exercício 461234567891011121314151617181920212223242526272829303132333435363738394041424344454748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

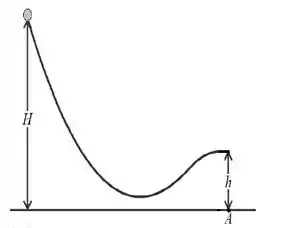
Na figura abaixo, uma pequena bola maciça de massa m e raio r rola sem deslizar, a partir do repouso, de uma altura H   =   6,0   m até deixar a parte horizontal no fim da pista a uma altura h   =   2,0   m do solo. Desprezando a resistência do ar, a que distância horizontal do ponto A a bola atinge o solo?

Dados:

I C M = 2 5 m r 2

(A) 3,8   m  

(B) 5,2   m  

(C) 6,0   m  

(D) 3,2   m  

(E) 4,8   m

Passo 1

Para descobrir o alcance da bola precisamos da sua velocidade no ponto A . E para achar a velocidade no ponto temos que usar a conservação da energia mecânica.

Como a bola é solta do repouso, temos que incialmente ela só tem energia potencial gravitacional.

E 0 = m g H

Já no ponto A , a bola tem energia potencial gravitacional, energia cinética de translação e energia cinética de rotação

Passo 2

E A = m g h + 1 2 m v 2 + 1 2 I ω 2

Como a bola rola sem deslizar, podemos relacionar velocidade angular com a velocidade de translação por

v = ω r → ω = v r

Assim

E A = m g h + 1 2 m v 2 + 1 2 I v r 2

Como I = ( 2 / 5 )   m r 2  

E A = m g h + 1 2 m v 2 + 1 2 2 5 m r 2 v 2 r 2 = m g h + 1 2 m v 2 + 1 5 m v 2

E A = m g h + 7 10 m v 2

Passo 3

Agora podemos usar a conservação de energia mecânica

E 0 = E A

m g H = m g h + 7 10 m v 2 →   m g H - h = 7 10 m v 2

v = 10 g H - h 7

Passo 4

Beleza!

Ao chegar no ponto A toda essa velocidade será horizontal! O alcance D será essa velocidade multiplicada pelo tempo de queda da bola.

O tempo de queda da bola é moleza! Basta só lembrar que

h = 1 2 g t 2

t = 2 h g

Assim o alcance D será dado por

D = v t = 10 g H - h 7 × 2 h g = 2 0 H - h h 7

Agora é substituir os valores numéricos

D = 20 H - h h 7 = 20 6 - 2 2 7

D ≈ 4,8   m

Resposta

(E)

Exercícios de Livros Relacionados

Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na Fig. 11-60, uma força horizontal constante F → de módulo 12N é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é 10k g , o raio é 0,
10.3E Um cilindro rola em uma rampa de inclinação θ = 30 ° . A) Calcule a aceleração angular do cilindro B) Calcule a força de atrito da rampa sobre o cilindro.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida