Dois discos A e B têm o mesmo momento de inércia, e estão em rotação com aceleração angular diferente de zero, conectados por uma correia que passa por suas periferias e não desliza sobre os discos. Os raios dos discos são e , respectivamente, conforme mostrado na figura.
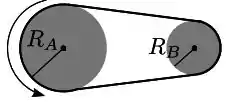
Comparando dois pontos situados na periferia de cada disco para um determinado instante, qual a única das quantidades abaixo que é a mesma?
(a) Módulo da velocidade linear.
(b) Módulo da aceleração angular.
(c) Módulo da velocidade angular.
(d) Módulo da aceleração linear.
(e) Componente radial da aceleração.
Passo 1
Qual é a relação entre os dois discos?
A relação é a partir da correia que conecta os dois.
A correia gira com uma certa velocidade. Como não há deslizamento entre a correia e os discos, os pontos na periferia dos discos terão a mesma velocidade que a correia.
Assim, os pontos na superfície dos dois discos terão a mesma velocidade entre si (em módulo):
Então, a grandeza que se conserva é o módulo da velocidade linear, letra (a).
Mas porque as outras grandezas não se conservam?
Passo 2
(c) Módulo da velocidade angular.
(b) Módulo da aceleração angular.
A velocidade angular está relacionada com a velocidade linear por:
Como as velocidades lineares são iguais:
As velocidades angulares serão diferentes, já que os raios são diferentes.
A aceleração angular também será diferente por consequência.
Passo 3
(e) Componente radial da aceleração.
(d) Módulo da aceleração linear.
A componente radial da aceleração, nada mais é do que a aceleração centrípeta, que é dada por:
Como os raios são diferentes, as acelerações centrípetas para os pontos na extremidade de cada disco serão diferentes:
Já a aceleração linear, é dada pela soma da aceleração tangencial com a aceleração centrípeta :
As acelerações tangenciais são as mesmas em módulo nos dois discos (velocidade lineares iguais), porém, as acelerações centrípetas são diferentes.
Assim, o módulo da aceleração linear será diferente para um ponto na extremidade de cada disco.
Resposta
Letra (a)