Um disco homogêneo de massa e raio está enrolado a um fio ideal que está preso ao teto e é solto a partir do repouso, no instante . O fio não desliza sobre a extremidade do disco, conforme mostra a figura.
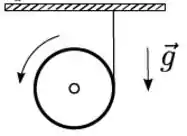
Sabendo que o momento de inércia do disco, em relação ao eixo perpendicular a ele que passa pelo seu centro de massa, é , podemos afirmar que:
(a) O centro de massa do disco desce com aceleração de módulo .
(b) O centro de massa do disco desce com aceleração de módulo .
(c) Enquanto o disco desce, a tração no fio é .
(d) O centro de massa do disco desce com aceleração de módulo .
(e) O centro de massa do disco desce com aceleração de módulo .
(f) Enquanto o disco desce, a tração no fio é .
(g) Enquanto o disco desce, a tração no fio é .
Passo 1
Dando uma olhada rápida nas alternativas, vemos que precisamos encontrar a aceleração do centro de massa do disco e também sua força de tração.
Vamos começar escrevendo a segunda lei de Newton:
Temos atuando sobre o disco duas forças, a força peso e a força de tração:
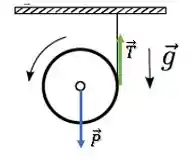
Além disso, a massa do disco é e sua aceleração do chamaremos de :
A força peso é:
Então ficamos com:
Pronto, já escrevemos a equação de forças para a translação.
Passo 2
Vamos escrever a segunda lei de Newton para rotação, agora:
Dá uma olhada novamente nas forças atuando sobre o disco:
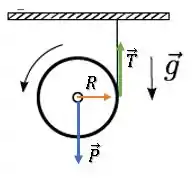
O torque da força peso será nulo, pois ele está aplicado no próprio eixo de rotação do disco.
Enquanto isso, a força de tração é perpendicular ao vetor posição, portanto, seu torque será o produto entre o módulo da força de tração e o módulo do vetor posição :
Assim, temos que:
Além disso, o enunciado nos deu que o momento de inércia de um disco é dado por:
Logo:
Existe mais uma relação que podemos usar nessa situação.
Como não há deslizamento entre o disco e o fio, temos obrigatoriamente que sua velocidade do centro de massa se relaciona com sua velocidade angular a partir da relação:
Substituindo na equação do torque resultante, temos:
Pronto, já escrevemos a equação dos torques para a rotação.
Passo 3
Temos, então, duas equações:
Vamos substituir primeiro o valor de da segunda equação na primeira para encontrar o valor de :
Cortando , temos:
Agora, vamos substituir o valor de de volta na primeira para encontrar o valor de :
Conseguimos o valor da aceleração do centro de massa do disco e da força de tração . Encontramos, então, que apenas a alternativa (a) está correta.
Resposta
Letra (a)