Uma bola de sinuca de raio rola sem deslizar do topo de um domo esférico com raio , onde . Considere que a velocidade inicial da bola de sinuca de raio é desprezível. Encontre o módulo da velocidade angular da bola de sinuca no momento em que ela perde contato com o domo.
Formulário: Momento de inércia da esfera .
(a)
(b)
(c)
(d)
(e)
Passo 1
Bom, para essa questão precisamos relacionar 3 coisas...
A primeira delas é que para a bolinha seguir uma trajetória circular, sua aceleração resultante deve ter exatamente o valor da aceleração centrípeta:
Onde é a velocidade da bola. Se a aceleração resultante tiver qualquer valor fora disso, a bola não seguirá mais a trajetória circular do domo.
A segunda delas é que a energia se conserva nesse sistema.
Isso acontece porque:
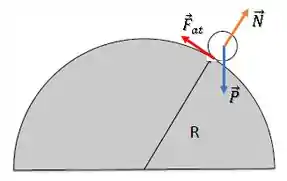
A força peso atuando na partícula é conservativa (não retira energia do sistema) e a força normal não vai realizar trabalho ao longo do deslocamento da bolinha por ser sempre perpendicular a ele, ou seja, ela também não retira energia do sistema.
Além disso, a força de atrito é estática (não há deslizamento), então seu trabalho também será zero , por isso, até a força de atrito, não vai retirar energia do sistema.
A terceira delas é que a bolinha desce o domo sem deslizar. Para isso acontecer, sua velocidade está relacionada com a sua velocidade angular por meio da relação:

Calma, eu sei que é muita coisa, mas segura na minha mão e vem comigo!
Passo 2
Vamos pensar na aceleração centripeta (primeira).
Quem é o raio da trajetória circular da bola?
Cuidado! Não é o raio do domo , pois não estamos tratando de uma partícula.
A bola tem uma certa dimensão, então temos que pegar a distância até seu centro de massa (centro da bola):
Esse é o valor “modelo” que a aceleração resultanteda bola deveria seguir para ter uma trajetória circular.
Passo 3
Ainda sobre essa hstória de força centrípeta, vamos analisar a bolinha em si.
Queremos calcular a aceleração resultante nela e ver até quando ela segue aquele “modelo” que achamos para aceleração centrípeta .
Então, vamos analisar as forças sobre a bolinha:
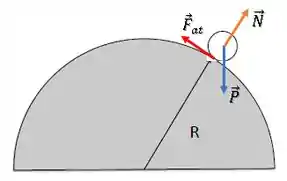
Queremos decompor essas forças na direção radial (direção do raio) e tangencial ao domo (mesma direção da velocidade da bolinha).
Repare que essas direções estão sempre mudando... diferente de um plano inclinado. Mas ainda assim, vamos relacionar com um ângulo , que vai variar:
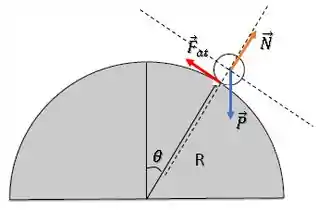
OBS: Esse ângulo poderia ser definido em outro lugar, desde que coerente com o que queremos. O ponto é, “putz não pensei em botar o ângulo exatamente alí”, relaxa que tem outras possibilidades.
e já estão nas direções que queremos analisar, só falta :
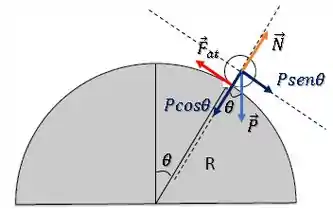
Vamos calcular a força resultante na direção radial, lembrando que ela deve apontar para o centro:
Pela segunda lei de Newton:
Agora, fazemos a ligação entre as coisas... para a bolinha seguir a trajetória circular do domo, sua aceleração deve ter o valor da centrípeta:
Passo 4
Agora, precisamos pensar um pouquinho!
Lá no início, a velocidade da bolinha é zero, então, o termo da esquerda começa bem menor que o termo :
Porém, quando a bolinha vai descendo, sua velocidade vai aumentando:
Já o ângulo vai aumentando, então o vai diminuindo:
O que vai justando essa diferença na equação é a força normal . Ela começa com valor alto e, à medida que o termo da esquerda e o vão se aproximando, a força normal vai diminuindo até chegar a zero.
Conclusão:
O instante limite onde a bolinha vai deixar de seguir a trajetória circular do domo é quando é zero:
Isso representa o instante onde a bolinha perde o contato com a superfície do domo, “descolando” dele.
Logo, na situação limite que queremos:
Substituindo o valor da força peso:
Passo 5
Agora vamos a nossa segunda relação.
Como a energia mecânica se conserva no sistema, podemos achar a velocidade da bolinha a partir da altura que ela deceu da situação inicial.
A bolinha começa em repouso, então sua energia inicial é toda potencial gravitacional :
A altura do centro de massa da bolinha no início é a soma dos raios do domo com o da bolinha :
Já nos instantes seguintes, a bolinha tem uma energia potencial gravitacional e uma energia cinétca :
Mas quem é essa altura da bolinha?
Podemos relacionar com o mesmo ângulo que determinamos lá no Passo 3.
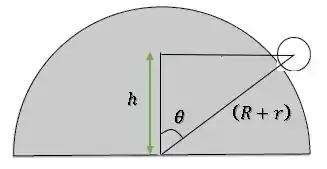
Então, conservando a energia mecânica, temos:
E quem vai ser a energia cinética da bolinha?
Passo 6
A bolinha tem uma velocidade de translação e uma velocidade de rotação .
Então, ela terá uma energia cinética de translação e uma energia cinética de rotação :
Do formulário, temos o momento de inércia da bolinha com relação ao seu centro de massa. É esse mesmo que queremos:
Mas podemos melhorar isso ai...
Lembra da nossa terceira relação?
A velocidade da bola está relacionada com a velocidade angular para que a bola não deslize:
Então:
Opaaa, o negócio ta ficando mais bonito!
Passo 7
Agora, já fizemos toda a parte mais complicada do problema.
Vamos começar uma seção de

Okay, não somos técnicos... mas vamos ainda vamos fazer as substituições.
Vamos rever tudo que achamos até agora:
Vamos jogar o valor da energia cinética (3) para dentro da conservação da energia (2):
Cortando a massa , temos:
Agora, vamos isolar o da aceleração centrípeta (1):
Substituindo na equação da energia, temos:
Usando novamente que :
Passando dividindo o termo que multiplica :
E assim, finalmente...

Desiste não, hahah
Finalmente, conseguimos que:
Ficamos com a letra (a).
Resposta
Letra (a)