A figura a seguir mostra um objeto uniforme que rola sem deslizar sobre um plano inclinado. O objeto possui massa , raio e momento de inércia ao redor do eixo de rotação. Sabe-se que quando o objeto é liberado do repouso a partir de uma certa altura , ele é lançado horizontalmente ao chegar à base do plano inclinado, tocando o solo a uma distância horizontal do ponto de lançamento.

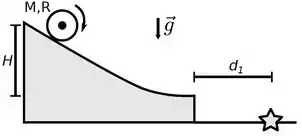
Considere, agora, que o objeto é substituído por outro, de mesma massa , mesmo raio e momento de inércia () ao redor do eixo de rotação. Nesse caso, quando solto do repouso da mesma altura , o novo objeto rola sem deslizar, e toca o solo a uma distância do ponto de lançamento.

Pode-se afirmar que:

Temos que, nos dois casos, o objeto deslizará do topo da rampa até a sua base, chegando com uma certa velocidade. Aquele objeto que chegar com maior velocidade na base da rampa é o que terá maior alcance!

Vamos olhar para o objeto primeiro

Temos pela conservação de energia mecânica

A energia no topo é puramente potencial gravitacional

Já a energia na base será cinética de translação e rotação!

Como o objeto rola sem deslizar, podemos relacionar a velocidade angular com a velocidade translacional

Assim, pela conservação da energia mecânica, temos

Da mesma forma, a velocidade na base do objeto é dada por

Assim como , temos que , ou seja, o alcance do corpo é maior que o alcance do corpo .

Outra forma de pensar nisso é que o corpo tem maior inércia de rotação, logo, uma maior parte da energia total acabará virando energia cinética rotacional, sobrando menos para a energia cinética translacional!