Um disco, um anel e uma esfera oca, todos de massa e raio são soltos simultaneamente a partir do repouso do topo de um plano inclinado que faz um ângulo com a horizontal. Existe atrito entre o plano inclinado e os objetos. Os objetos rolam sem deslizar plano abaixo.
Assinale falso ou verdadeiro às seguintes afirmações. Neste item não é necessário justificativa.
As forças de atrito e da gravidade nos objetos apontam na mesma direção e em sentidos opostos;
O disco chegará primeiro na base do plano inclinado por que tem o menor momento de inércia;
O anel chegará primeiro na base do plano inclinado por que tem o maior momento de inércia;
Como todos tem a mesma massa e mesmo raio, todos chegarão juntos na base do plano inclinado;
Se não existisse atrito todos chegariam juntos na base do plano inclinado.
Passo 1
Como toda boa questão com várias afirmações, vejamos uma de cada vez (ou algumas juntas).
“As forças de atrito e da gravidade nos objetos apontam na mesma direção e em sentidos opostos”
FALSO
Ele afima que a força de atrito e de gravidade seriam opostas uma à outra (“apontam na mesma direção e em sentidos opostos”).
Vejamos como ficariam as forças nesse caso:
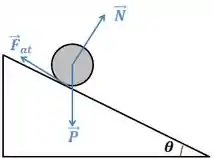
A força peso está sempre na direção do centro da Terra, enquanto a força de atrito é oposta ao movimento (ao longo da rampa). Assim, elas não tem mesmo direção e logo nem podemos falar em “sentidos opostos”.
Por isso, essa afirmação é falsa.
Passo 2
“O disco chegará primeiro na base do plano inclinado por que tem o menor momento de inércia”
VERDADEIRO
“O anel chegará primeiro na base do plano inclinado por que tem o maior momento de inércia”
FALSO
“Como todos tem a mesma massa e mesmo raio, todos chegarão juntos na base do plano inclinado”
FALSO
A explicação pras três afirmações é a mesma. Vamos observar como ficariam as equações do movimento nesse caso.
A segunda lei de Newton para o movimento do centro de massa fica:
Podemos colocar os eixos ao longo da rampa, e decompor as forças em suas componentes.
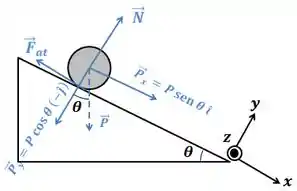
Teremos então para cada componente
Enquanto para o movimento de rotação:
Como é perpendicular ao raio no ponto de aplicação, temos:
Pela cinemática do problema, se considerarmos apenas rolamento, teremos:
Daí vale que:
Podemos substituir esse resultado na equação do movimento ao longo do eixo (afinal, o anel, disco ou esfera não se move ao longo do eixo que a gente definiu).
Essa equação nos mostra que a aceleração é constante para cada objeto (já que o momento de inércia depende apenas de sua geometria), por isso, como eles partem do repouso, temos uma situação de MUV.
Como os três objetos percorrem a mesma rampa, quanto menor a aceleração, maior o tempo. Da equação da aceleração, quanto maior o momento de inércia, menor a aceleração.
Precisamos saber então o momento de inércia de cada um dos corpos.
Passo 3
Os momentos de inércia do disco (equivalente ao do cilindo), do anel (equivalente à casca cilíndrica) e da esfera oca ao redor de seus centros de massa nós já temos da teoria (no caso da prova, eles também eram dados no formulário):
Nota-se que:
Logo, pela discussão anterior:
Passo 4
“Se não existisse atrito todos chegariam juntos na base do plano inclinado”
VERDADEIRO
Se não existisse atrito, não teríamos nenhuma força gerando um torque. Logo, nosso problema seria apenas de deslizamento.
Nesse caso, as leis de Newton ficariam:
A aceleração então seria a mesma para o disco, o anel e a casca esférica, o que faria com que eles levassem o mesmo tempo para chegar na base do plano.
Resposta
As forças de atrito e da gravidade nos objetos apontam na mesma direção e em sentidos opostos;
O disco chegará primeiro na base do plano inclinado por que tem o menor momento de inércia;
O anel chegará primeiro na base do plano inclinado por que tem o maior momento de inércia;
Como todos tem a mesma massa e mesmo raio, todos chegarão juntos na base do plano inclinado;
Se não existisse atrito todos chegariam juntos na base do plano inclinado.