Um cilindro homogêneo de massa e raio sobe um plano inclinado de um ângulo em relação à horizontal sob a ação de uma força constante, como mostra a figura abaixo. O cilindro parte do repouso e sua velocidade angular aumenta com o tempo. Sabe-se que o cilindro rola sem deslizar e que seu momento de inércia em relação a um eixo perpendicular que passa pelo seu centro de massa é .
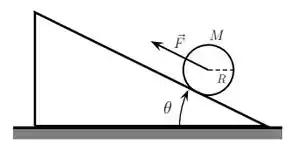
Dado:
b) Determine a força de atrito (módulo, direção e sentido) que o plano excerce sobre o cilindro.
c) Determine a velocidade do centro de massa do cilindro após o mesmo ter subido uma altura h, em relação à sua posição inicial.
Passo 1
Na letra (b), queremos o valor da , além de sua direção e sentido.
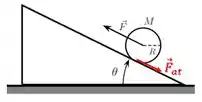
Dá uma olhada na figura de novo:
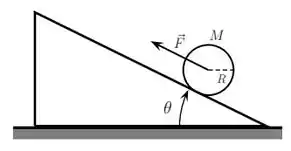
A força (aplicada no centro de massa do cilindro) puxa ele para cima, então a tendência de deslizamento é para cima.
A força de atrito vai atuar contra essa tendência de deslizamento, logo estará para baixo:
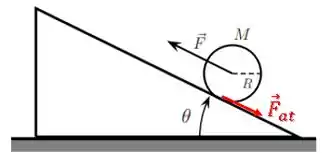
Podemos ter a certeza da direção da força de atrito, pois ela é a única força que gera torque no cilindro. Assim, ela deve fazê-lo entrar em rotação no sentido horário (subir a rampa).
Passo 2
Agora, vamos calcular o módulo da .
Para isso, vamos escrever as equações de translação e de rotação para esse corpo, e com elas, conseguimos resolver o sistema e achar a .
Quais são as forças atuando no cilindro?
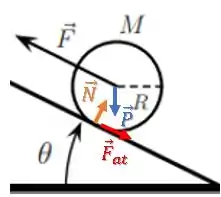
Passo 3
Rotação:
Pela segunda lei de Newton para rotação:
O torque resultante é a soma dos torques de cada forças:
Vamos calcular com relação ao eixo de rotação, que passa pelo centro de massa:
O torque da força peso é zero pois ele está aplicado no centro de massa. O torque da força é zero pelo mesmo motivo.
Já o torque da força normal , será:
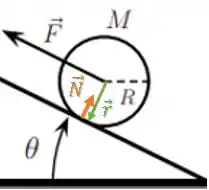
O produto vetorial é zero pois os vetores são paralelos.
Assim, o torque da força normal é nulo, pois a força está na direção do centro de massa.
Por último temos a força . Seu torque será dado por:
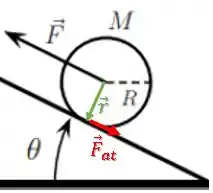
Como os vetores são perpendiculares, o módulo do torque será:
Substituindo todos esses valores na equação dos torques, temos:
Passo 4
Translação:
Vamos decompor a força peso nas direções paralela e perpendicular à rampa:
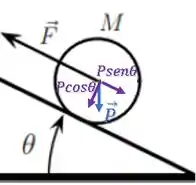
Então, ficamos com as seguintes componentes:
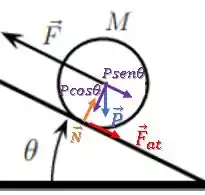
Na direção paralela à rampa, temos:
Podemos escrever a equação de forças na direção perpendicular à rampa, porém, não vamos precisar dela...
Isso porque a não se relaciona com a força normal , pois ela não necessariamente apresenta valor máximo:
Passo 5
Bom, temos as seguintes equações:
Além delas, temos também a relação de rolamento sem deslizamento:
Podemos substituir o valor de na segunda equação:
Já na primeira equação, podemos substituir o valor do momento de inércia do cilindro:
Agora, temos esse sistema aqui:
Somando as duas equações, temos:
Passo 6
Na letra (c), queremos a velocidade do centro de massa do cilindro após ele subir uma altura .
Podemos resolver esse item por energia, atravé do teorema trabalho-energia cinética:
Sendo o trabalho resultante de todas as forças e a energia cinética sendo a soma da energia cinética de rotação com a de translação .
Porém, como já temos a força de atrito do item (b), um outro caminho é encontrar a aceleração sobre o cilindro e a partir dela, encontrar a velocidade.
Passo 7
Como o cilindro parte do repouso, basta descobrirmos o seu deslocamento que conseguimos achar sua velocidade, por meio de Torricelli:
Para achar esse deslocamento , vamos usar a inclinação da rampa:
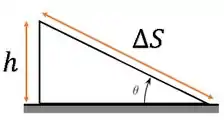
Achamos quanto o cilindro precisa se deslocar ao longo da rampa para subir uma altura .
Passo 8
Aplicando Torricelli:
A velocidade inicial é zero (parte do repouso):
Substituindo os valores de e de , temos:
Assim, temos que a velocidade é:
Resposta
(b)
(c)