Um balde pequeno de massa está preso a uma corda de massa desprezível que, por sua vez, encontra-se enrolada em torno de uma roldana cilíndrica de massa e raio como mostrado na figura. A roldana gira em torno de seu eixo de simetria. O balde é liberado a partir do repouso de uma altura do solo. No movimento que se segue, a corda se desenrola do cilindro sem deslizamento.
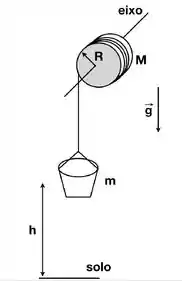
A. Adote um sistema de coordenadas, esboce o diagrama de forças para o balde e para a roldana e escreva todas as forças explicitamente no sistema de coordenadas adotado.
B. Baseado nas forças identificadas em (A), escreva as equações de movimento para o balde e para a roldana.
C. Determine o vetor aceleração do CM do balde. Calcule a magnitude dessa aceleração para os casos extremos em que e .
D. Determine a velocidade com que o CM do balde atinje o chão. Considere o balde como uma partícula pontual.
E. Verifique explicitamente a validade do teorema do trabalho-energia cinética para o sistema “balde+roldana+corda”.
Passo 1
(A)
Beleza, vamos lá!
Temos que fazer um desenho com todas as forças.
Ambos tem massa e sofrem atração gravitacional, então ambos tem peso.
Ambos tem um fio, então ambos tem tração.
Só isso?
Não! Alguma coisa tem que segurar a roldana lá. O pino tá preso em algum lugar, e ele que tá segurando a roldana, vamos chamar essa força que segura a roldana de .
Show! Então vamos desenhar:
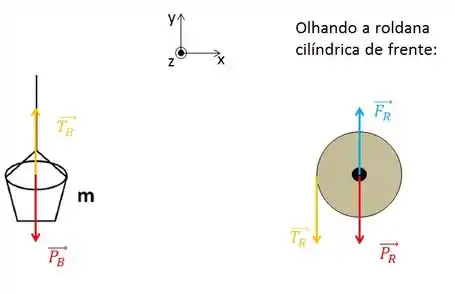
Agora, só uma observação: Podemos dizer alguma coisa em relação as trações e ?
Sim! A massa da corda é desprezível, isso implica que a intensidade da trações nos pontos diferentes da corda são iguais. Ou seja:
Mas é só o módulo tá? Olha que uma tá apontando pra cima e outra pra baixo!
Ele pediu pra gente especificar um eixo de coordenadas, e escrever todas as forças explicitamente, então vamos lá:
Para o balde:
Para a roldana:
Beleza! Sucesso?
Passo 2
Agora ele quer as equações de movimento. Ou seja, aplicamos a segunda lei de newton para cada um dos corpos.
Para o balde:
Show!
Agora, para a roldana! Como a roldana está fixa, o CM dela tem aceleração nula:
Show, então essa é a rquação de movimento para o CM da roldana.
Além disso, como a roldana tá girando, já que o fio tá se deenrolando dela, temos uma rotação ali, então:
Temos três forças sendo aplicadas na roldana: o peso, a tração e a força de sustentação. Quais delas produzem torque, ou seja, quais delas podem provocar uma rotação na roldana?
Se você olha lá na figura, o peso e a força de sustentação são aplicadas no CM da roldana, assim, não importa o quão forte eles sejam, mas a roldana não gira por ação deles.
Já a tração é diferente, percebe? Ela tá na borda. Essa produz rotação! Então o torque resultante é devido a ela!
Lembrando que esse é o braço de alavanca da força, ou seja é a distância entre o eixo de rotação até o ponto em que a força tá sendo aplicada, nesse caso é
Então:
O momento de inércia para um cilindro girando em torno de um eixo que passa pelo CM vale:
Então:
Maravilha!
Passo 3
(C)
Agora é só uma continuação da letra B, porque ele pede a aceleração do CM do balde. Então é só brincar com as equações do CM e isolar a aceleração.
A aceleração do CM do balde é a mesma aceleração que o fio vai se desenrolando lá na borda da roldana, então vamos usar essa última equação do passo 2:
Isolando a aceleração:
Usando o fato do rolamento ser sem deslizamento, temos:
Beleza, acabou?
Não!
Ainda não sabemos que é a tração.
Vamos usar então a equação de translação do balde:
Isolando a tração:
Agora, é substituir na equação que a gente tinha:
Maraviha, agora é só ajeitar e teremos:
Suave!
Vamos ver os casos extremos que o enunciado falou pra gente, que e.
Vamos reescrever:
Ou seja, estamos analisando o caso em que a roldana é muito mais pesada que o balde. Olhando pra equação:
Se a parte do denominador for muito grande, então a fração vai pra zero, ou seja a aceleração vai a zero.
Já para o segundo caso:
Então .
Estamos analisando o caso em que o balde é muito mais pesado que a roldana.
Olhando pra equação:
Temos que:
Passo 4
(D)
Queremos a velocidade com que o balde chega ao chão.
Então, lá no enunciado ele fala que o balde sai do repouso, então . Nós não sabemos nada sobre o tempo que demorou essa descida, mas sabemos o quanto o balde andou, ou seja, :
Usando Torriceli:
Substituindo os valores:
Show!
Passo 5
(E)
Queremos verificar o teorema trabalho energia cinética:
Então, primeiro vamos calcular a , entre o momento em que o bloco tá parado a uma altura e quando ele chega no solo com uma velocidade , que a gente acabou de calcular na letra D. E como o nosso sistema é balde+corda+roldana, não podemos esquecer da energia cinética de rotação da roldana.
O momento de inércia para um cilindro girando em torno de um eixo que passa pelo CM vale:
E como rola sem deslizar, podemos escrever:
Então:
Substituindo a velocidade que achamos na letra D:
Ajeitando isso:
Colocando em evidência, podemos simplificar e ficamos com:
Agora vamos calcular o trabalho de todas as forças durante a descida do balde e ver se o resultado é igual a esse aí, se for, aí tá show! O teorema trabalho energia vai ser válido. Então vamos lá, escrevendo o trabalho de todas as forças que atuam no sistema balde+fio+roldana:
Agora, vamos com calma:
Vamos analisar e , que são os trabalhos realizados pelo peso da roldana e pela força de sustentação da roldana. Então, durante o deslocamento do balde, essas forças não alteram a energia cinética do sistema. Já que é só o balde está se movendo.
Agora, vamos analisar e . A gente viu que as trações tem módulos iguais, mas estão apontando em sentidos opostos. Então o trabalho de uma vai ser menos o trabalho da outra. Aí eles vão zerar.
Então, só nos resta o trabalho do peso do bloco:
Maravilha! O resultado é igual ao da variação da energia cinética que a gente encontrou. Então o teorema é válido!
Resposta
(A)
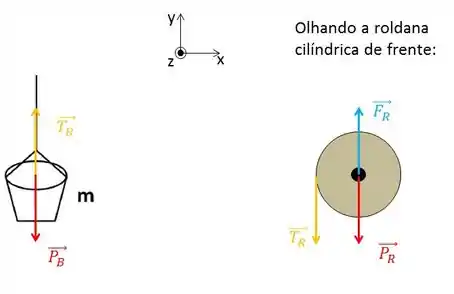
Para o balde:
Para a roldana:
(B) Para o balde:
Para a roldana:
(C)
(D)
(E) Verificação