Na figura abaixo, temos dois cilindros 1 e 2 que se movem puxados por uma força . Os dois cilindros são idênticos, e seus centros estão ligados por uma corda ideal. Os rolamentos são sem deslizamento. Podemos afirmar que:
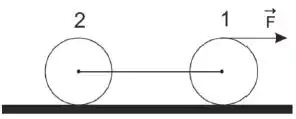
a) A força de atrito sobre o cilindro 1 está no mesma direção e sentido da força , e a força de atrito sobre o cilindro 2 está na mesma direção e sentido oposto a esta força.
b) As forças de atrito sobre os cilindros 1 e 2 estão na mesma direção e mesmo sentido da força .
c) A força de atrito sobre o cilindro 1 está na mesma direção e sentido oposto ao da força , e a força de atrito sobre o cilindro 2 está na mesma direção e mesmo sentido desta força.
d) As forças de atrito sobre os cilindros 1 e 2 estão na mesma direção e mesmo sentido, oposto ao da força .
e) N.D.A.
Passo 1
Vamos supor que as duas estão para o mesmo lado como na figura abaixo:
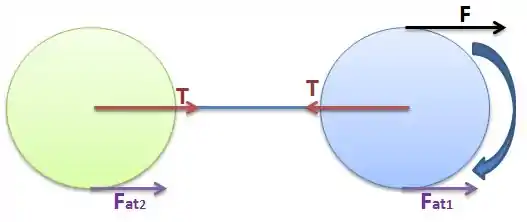
Na figura da direita, vemos que a força gera um torque que faz a roda girar no sentido horário, sua parte inferior vai tocar no chão “empurrando-o” para trás, desta forma a Força de Atrito será pra frente.
Já no bloco 2 o único torque é da Força de atrito, mas daí a gente não sabe qual a direção realmente dele. Então, vamos analisar as coisas...
Passo 2
Vamos chamar ele, o Newton:
Pela Segunda Lei de Newton, teremos:
Para o Cilindro 1:
Para o Cilindro 2:
Somando tudo, teremos:
Passo 3
Agora, usando o Newton para rotação, teremos:
Para o Cilindro 1:
Para o Cilindro 2:
Cortando tudo o que tem direito e e substituindo o que der,teremos:
Substituindo na ultima equação do passo anterior, vai ficar:
Como é a força que puxa o sistema todo, vencendo os atritos e tudo, ela tem que ser maior que o , pois se não tivesse tudo isso a aceleração seria maior que a nossa .
Logo:
E assim...
Isso significa que ela está apontando para a esquerda, o sentido oposto do que a gente colocou no início.
Resposta
Letra A