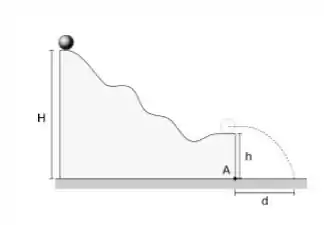
Uma bola maciça rola suavemente (sem deslizar) a partir do repouso, começando de uma altura , até deixar a parte horizontal no fim da pista, a uma altura , conforme a figura ao lado. Dado que o momento de inércia de uma bola maciça de massa M e raio em relação ao centro de massa é e , responda:
(a) Qual a velocidade do centro de massa da partícula no fim da pista?
(b) Usando a resposta do item anterior, calcule a que distância horizontal do ponto a bola toca o chão.
Passo 1
(a) Podemos achar a velocidade no fim da pista usando conservação da energia mecânica. Escolhendo o zero da energia potencial na altura com relação ao chão, igualamos a energia mecânica na altura com a energia mecânica na altura :
onde a energia potencial é calculada na altura , pois o ponto de referência é na altura e é a energia cinética de translação do centro de massa mais a energia cinética de rotação em torno do centro de massa. Como a bola não desliza, temos que . Usando esta equação e que em , obtemos
Passo 2
(b) Este item pode ser resolvido usando as equações para um lançamento horizontal a partir da altura . Escolhendo a origem do sistema de coordenadas no ponto , com positivo para a direita da figura e positivo para cima, notamos que a velocidade inicial do movimento é . Portanto, a distância horizontal pode ser calculada via . Podemos encontrar usando a equação de queda livre
Assim, temos que:
Resposta
(a)
(b)