Uma lata vazia de altura , raio e massa , com tampa, parte do repouso e rola sem escorregar por um plano inclinado de angulo e comprimento . Considere conhecido que o momento de inércia de um disco de massa e raio em relação à um eixo perpendicular que passa pelo seu centro é .
a)Qual é o momento de inércia da lata, , em relação ao seu eixo de simetria? O resultado deve ser dado como função de . Considere a lata como sendo um cilindro com duas tampas, com densidade superficial homogênea.
b) Calcule a força de atrito sobre a lata em termos de ;
c) Calcule a aceleração do centro de massa e a aceleração angular da lata;
d) Calcule velocidade angular da lata ao chegar ao final da rampa;
e) Qual o trabalho realizado pela força de atrito? Justifique.
Passo 1
a)
Temos um cilindro deitado de massa total , como na figura abaixo:

Como a massa M é da borda+ tampa, teremos que calcular a massa de cada parte.
Como a lata é feita de um material só, podemos relacionar a massa com a área da lata.
Temos que:
E assim:
Pra saber só a massa da lateral, por regras de três simples, teremos:
Já a massa de uma tampa será:
Passo 2
Agora a gente calcula o Momento de Inércia. Na Tampa a gente viu que é e no cilindro inteiro . Desta forma, substituindo as massas, teremos:
Passo 3
b)
Isolando as forças, teremos:
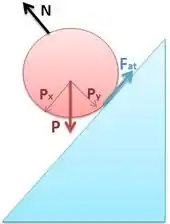
Pela Segunda Lei de Newton...
Isolando o ...
E agora utilizando a mesma lei para a Rotação, vai ficar:
Passo 4
Como , teremos:
Ah, agora é só um pouquinho de algebrismo:
Passo 5
c)
Voltando lá na primeira equação que encontramos no Passo 3 , teremos:
Agora que a gente já sabe a é só substituir:
Passo 6
O é molezinha demais, é só utilizar...
Passo 7
d)
Como ele parte do repouso podemos calcular a velocidade angular como
Além disso, utilizando as equações da cinemática, teremos:
Passo 8
O trabalho da força de atrito é nulo, pois no rolamento sem deslizamento a força de atrito é estática e o ponto em que o cilindro toca a supercífie tem velocidade nula. :D
Resposta
a)
b)
c)
d)
e)