Aplica-se uma força de 3000N a um rolo compressor que tem a forma de um cilindro maciço uniforme de raio 0,5m e massa 1000kg, conforme a figura. O cilindro rola sem deslizar sobre uma superfície horizontal. A aceleração do centro de massa e coeficiente de atrito mínimo para impedir o deslizamento valem , respectivamente:
a)
b) 3
c)
d)
e)
Passo 1
Fazendo uma figurinha melhor, haha:
Isolando as forças, teremos:
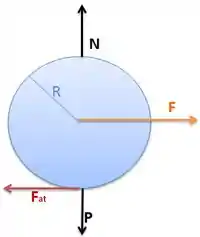
Passo 2
Achando as equações de Newton do sistema, teremos:
Na vertical:
Na horizontal:
Como ele quer o coeficiente mínimo, temos que garantir que a força de atrito seja estática em seu valor máximo, ou seja:
Torque:
Como as forças têm linha de atuação que apontam para o centro da face do cilindro, não realizam torque, logo, somente a força de atrito causará torque:
Passo 3
Sabemos que o nosso é dado por:
Além disso, “sabemos”, ou deveríamos saber que o momento de inércia do cilindro com seu eixo de rotação no centro da face é dado por:
Passo 4
Substituindo esse último resultado na equação de Newton com as forças verticais, teremos:
Como :
Resposta
d)