Uma esfera sólida de massa e raio rola sem deslizamento ao longo da trajetória mostrada na figura. Ela inicia o movimento partindo do repouso quando a esfera está a uma altura acima da parte inferior do loop de raio , muito maior do que .
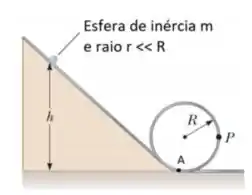
a) Qual o módulo da velocidade quando a esfera chega no ponto A?
b) Qual o módulo da velocidade angular na base, ponto A, do plano inclinado?
c) Desenhe o diagrama de corpo livre da esfera quando esta estiver no ponto P.
d) Qual é o valor mínimo de (em termos de ) para que a esfera complete o loop?
Passo 1
Fala galerinha, beleza? Partiu resolver esse problema sobre conservação da energia mecânica?
Para gente resolver o item (a), o segredo é aplicar a conservação da energia mecânica considerando o ponto de partida e o ponto A:
Inicialmente, a esfera tinha apenas energia potencial gravitacional:
No ponto A, a esfera tem apenas energia cinética. Todavia, temos que tomar um cuidado para não esquecer a energia cinética de rotação:
O momento de inércia de uma esfera é
Como a esfera rola sem deslizar, temos , de modo que
Portanto,
Passo 2
No item (b), ele pede :
Logo,
Passo 3
No item (c), ele cobra o diagrama de força sobre a esfera quando ela se encontra no ponto P. A seguir fazemos esse desenho:
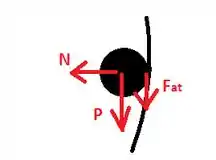
É muito importante que você não esqueça do atrito! A esfera só consegue rolar sem deslizar devido a um torque em torno do centro de massa e isso só é possível por causa da força de atrito. Vale destacar que, como a velocidade do ponto de apoio da esfera na superfície é nula, a força de atrito é estática e não realiza trabalho. Por isso pudemos brincar com a conservação de energia sem problemas no passo 1.
Passo 4
Vamos fechar o problema com o item (d). Vamos calcular primeiro a velocidade mínima que a esfera deve ter no topo do loop para não perder contato com a pista.
No topo do loop, tanto a normal quanto o peso apontam para o centro da trajetória, de modo que a força centrípeta pode ser escrita como
Ou ainda,
Na situação limite em que a esfera perde contato com a pista, temos e , de modo que
Usando conservação de energia, temos que
Como discutido no passo 1, temos que
Já na situação final, temos
Repare que no topo da trajetória temos tanto energia potencial como cinética. Como visto no passo 1,
Logo,
Substituindo , temos que
Assim,
Essa é a altura mínima que a esfera deve ser abandonada para que ela consiga completar o loop sem perder contato com a pista 😉!