Um bloco de massa inicialmente em repouso e a uma altura desliza para baixo sobre a superfície de um plano inclinado que faz um ângulo com a horizontal. O plano inclinado permanece em repouso enquanto o bloco desliza sobre ele. Depois de ter chegado à base do plano o bloco continua a deslizar por uma distância ao longo de uma superfície horizontal até entrar em repouso. O coeficiente de atrito cinético é o mesmo entre o bloco e ambas as superfícies. Utilize obrigatoriamente a Lei de Conservação de Energia.
Dados:
a) Determine o valor da energia potencial que o bloco possui assim que ele chega à superfície horizontal.
b) Determine o valor da energia cinética que o bloco possui assim que ele chega à superfície horizontal.
c) Determine a distância percorrida pelo bloco ao longo da superfície horizontal até ele entrar em repouso.
Passo 1
Na letra (a), queremos a energia potencial gravitacional do bloco na superfície horizontal.
Bom, a energia potencial gravitacional depende sempre de uma referência de energia potencial zero.
Geralmente traçamos essa referência no ponto mais baixo da trajetória, porém isso é opcional.
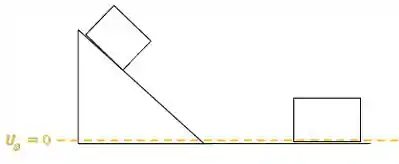
Assim, temos que a energia potencial gravitacional do bloco é zero de acordo com o nosso referencial:
Passo 2
Na letra (b), queremos a energia cinética do bloco assim que ele atinge o solo.
Uma boa maneira de encontrar a energia cinética é relacionando ela com o trabalho das forças sobre o corpo (Teorema Trabalho-Energia Cinética):
Esse teorema, parte da conservação da energia (exigida no enunciado). Porém, não significa que a energia do bloco se conserva, pois há uma força de atrito.
Entretanto, a energia do sistema total se conserva, ou seja, a energia perdida pelo bloco é a energia ganha pelo meio.
Eu sei, fica um pouco abstrato, mas dá uma olhada como vamos utilizar esse teorema.
Esse teorema diz que o trabalho resultante sobre o corpo (todas as forças) é igual a variação de energia cinética.
Como o corpo parte do repouso, sua energia cinética inicial é nula:
Passo 3
Beleza, mas quem é o trabalho resultante sobre o corpo?
É o trabalho de todas as forças sobre ele:
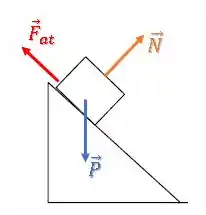
Já de cara, podemos cortar o trabalho da força normal .
Isso porque essa força é sempre perpendicular ao deslocamento, logo seu trabalho é zero:
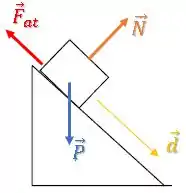
Então, ficamos com:
Vamos calcular esses dois trabalhos.
Passo 4
O trabalho da força peso é dado pela variação de altura do bloco:
Como o bloco está descendo, a força peso está a favor do deslocamento, e por isso, seu trabalho é positivo:
Passo 5
Já a força de atrito atua contra o deslocamento (mesma direção e sentido oposto), portanto seu trabalho é negativo:
Mas precisamos descobrir quem é essa força de atrito e quanto vale o deslocamento .
Vamos começar com a . A força de atrito cinético é dada por:
E essa força normal , nós podemos encontrar fazendo o equilíbrio de forças na direção perpendicular à rampa:
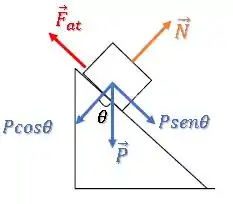
Então, a força de atrito é:
Mas e o deslocamento ?
Bom, sabemos a inclinação da rampa e a altura vertical que o bloco desceu, então, conseguimos calcular a distância na direção da rampa:

Assim, juntando as expressões de e , temos que o trabalho da força de atrito é:
Passo 6
Beleza, agora que já temos o trabalho da força peso e de atrito, podemos voltar por teorema:
Colocando em evidência, temos:
Substituindo os valores:
Então, a energia cinética no instante em que o bloco chega ao chão é aproximadamente:
Passo 7
Na letra (c), queremos saber a distância percorrida até que o bloco pare.
Novamente, vamos utilizar o teorema:
Mas agora, vamos considerar o instante inicial a partir do momento que o bloco atinge o chão, pois já calculamos esse valor no item (b):
E o instante final, sendo o instante onde o bloco volta ao repouso, ou seja, sua energia cinetica é nula:
Passo 8
E o trabalho resultante sobre o bloco será o trabalho das forças peso, normal e de atrito:
Como tanto a força peso , quanto a força normal não realizam trabalho, resta apenas o trabalho da força de atrito:
O trabalho da força de atrito ainda é dado pela expressão:
Entretando, o módulo da força de atrito se alterou, já que a força normal também se alterou:
Como há um equilíbrio na vertical, temos que:
Então:
Substituindo na expressão do trabalho, temos:
Passo 9
Agora, podemos voltar ao teorema:
Cortando e o sinal negativo, temos:
Essa é a distância que o bloco leva até parar.
Resposta
(a)
(b)
(c)