Um bloco A de massa está conectado a um bloco B de massa e a uma mola ideal de constante elástica . A corda e a roldana são também ideais. O bloco A está sobre uma superfície horizontal e o bloco B está sobre um plano inclinado que faz com a horizontal um ângulo, e ambas as superfícies oferecem aos blocos atrito de mesmo coeficiente cinético. Inicialmente os blocos estão em repouso e a mola está relaxada. Devido às forças em jogo, o sistema sai do repouso e vai se deslocar uma distância até parar momentaneamente. Determine, em termos dos parâmetros pertinentes:

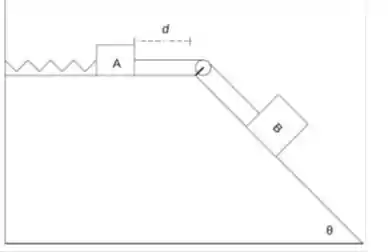
(a) o trabalho da força elástica realizado pela mola sobre o sistema dos blocos nesse deslocamento;

(b) o trabalho realizado pela força gravitacional sobre o sistema;

(c) os trabalhos e realizados pelas forças de atrito e pelas forças normais sobre o sistema.

Considere agora os seguintes valores: , , e

(d) Determine o valor de .

(b) o trabalho realizado pela força gravitacional sobre o sistema;

Como queremos o trabalho da força peso no sistema temos que analisar tanto o corpo A quanto o corpo B.

O peso também é uma força conservativa, então o seu trabalho só depende das posições inicial e final.

Como no corpo A não há variação de altura temos que

Já para o corpo, temos variação de altura. Podemos calcular o trabalho da força peso de duas formas diferentes, uma é igual ao que fizemos acima, mas também podemos usar a definição de trabalho. Como já fizemos usando a variação da energia potencial gravitacional, vamos usar agora a definição. Então:

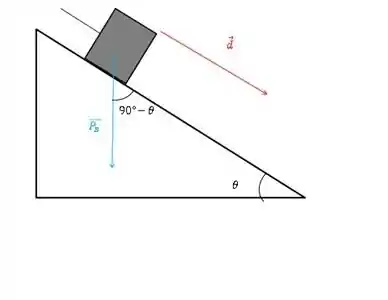
Note que o ângulo entre os vetores força peso e deslocamento é

Só que . Então

Note que nada mais é do que a variação de altura, ou seja, tanto faz usar a definição de trabalho ou que ele é menos a variação de , para forças conservativas. Você escolhe!

(c) os trabalhos e realizados pelas forças de atrito e pelas forças normais sobre o sistema.

Primeiro vamos ver a normal.

Bom, em ambos os corpos, o trabalho da normal vai ser zero, porque a força normal é perpendicular ao deslocamento durante todo o percurso.

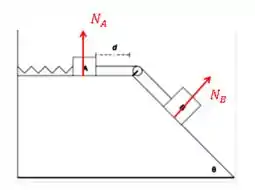
E o trabalho das forças de atrito... Primeiro para o corpo A:

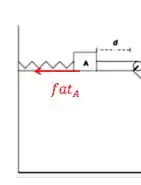
O deslocamento está horizontalmente para a direita, já a está horizontalmente para esquerda, pois ela é contra o movimento. Com isso, o ângulo entre eles é .

Eita... quem é a normal em A? Pensa aqui comigo. O corpo A não se move pra cima e pra baixo. Nessa direção vertical, as únicas forças que atuam são o peso e a normal, e como não a movimento nessa direção, a resultante é zero, e, portanto

Beleza.

Vamos para o corpo B.

O ângulo entre a normal e o deslocamento continua zero, então o trabalho dela também será.

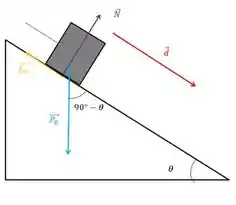
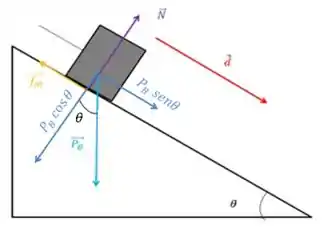
E a força de atrito é oposta ao sentido do deslocamento. Então

Agora que vem um detalhe diferente do A. Não podemos dizer que o peso é igual ao normal. Na verdade, Que é a componente do peso na mesma direção da normal.

Considere agora os seguintes valores: , , e

(d) Determine o valor de .

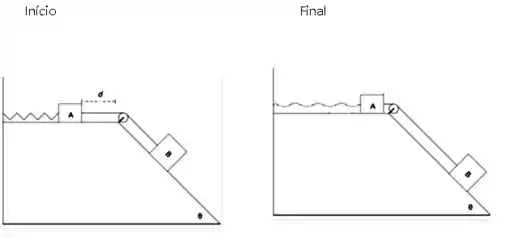
Vou colocar a imagem do enunciado aqui de novo para gente lembrar.

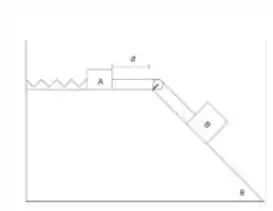
Vamos lá. O sistema sai do repouso e anda uma distância em uma superfície com atrito e depois ele para novamente. Ou seja, a variação da energia cinética foi zero. Mas durante esse percurso de houve dissipação de energia, por causa da força de atrito atuando.

Usando o teorema trabalho energia podemos relacionar todos esses trabalhos que já calculamos nos itens anteriores, pois calculamos o trabalho de toas as forças no sistema, e é justamente sobre isso que o teorema trabalho energia cinética trata.

Substituindo tudo:

Pelos valores dados, encontramos que