Um bloco de massa repousa sobre uma superfície horizontal sem atrito e está preso a uma mola também na horizontal de constante elástica cuja outra extremidade é mantida fixa. A mola está relaxada e o bloco está em repouso na posição inicial quando uma força horizontal é aplicada no sentido do eixo positivo. O gráfico abaixo mostra como a energia cinética do bloco varia em função da posição durante a aplicação das forças.
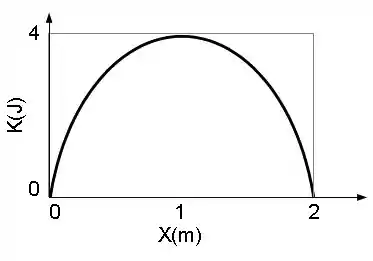
(a) Escreva o teorema Trabalho-Energia Cinética para as forças que atuam no bloco.
(b) Calcule o trabalho realizado pela mola de até
(c) Calcule o trabalho realizado pela força de até .
Passo 1
(a)Lembrar do teorema Trabalho-Energia Cinética
O teorema Trabalho-Energia Cinética tem uma expressão simpática, que é essa aqui:
Ou seja, o trabalho total é igual a variação da energia cinética, beleza? Mas quem é o trabalho total? Bem, as forças atuando são a força que foi aplicada no bloco, mas existe também a força que a mola faz se opondo ao movimento, não se esqueça! Então, teremos:
Passo 2
(b)Calcular o trabalho da mola
Quando aplicamos a força no bloquinho, a mola vai atuar dificultando o movimento. Como a força da mola e o deslocamento estão em sentidos contrários, sempre que for esse o caso, vamos considerar trabalho negativo, beleza?
De até , tivemos uma deformação de , porque em a mola estava relaxada, lembra? Então:
Passo 3
(c)Calcular o trabalho da força aplicada
Para calcular esse trabalho, a gente tem que ficar atento no gráfico. Não usamos ele até agora, então agora é a hora! Veja que em e a energia cinética é a mesma! Então, vamos ter: