
Um bloco de massa é solto do repouso de uma altura (posição A) na pista ilustrada na figura abaixo. A pista é sem atrito, a menos do trecho BC de comprimento . O bloco chega à mola de constante elástica desconhecida e a comprime de uma distância até chegar a um repouso momentâneo. As respostas devem ser dadas em função das variáveis do problema ( e ) e da aceleração da gravidade . Explicite em todos os itens os teoremas utilizados.
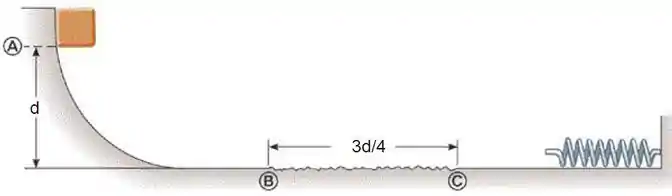
a) Determine a energia cinética com que o bloco chega à posição B e o trabalho realizado pela força da gravidade da posição A até a posição B.
b) Sabendo que o bloco chega à posição C com metade da velocidade com que ele chegou em B calcule trabalho realizado pelo atrito e o coeficiente de atrito cinético do trecho BC.
c) Determine o trabalho realizado pela mola desde quando ela estiver relaxada até quando estiver totalmente comprimida. Determine a constante elástica da mola.
d) O bloco agora retorna empurrado pela mola. Determine a altura máxima que ele alcança.
Passo 1
a)
A letra a) é uma simples aplicação da conservação da energia mecânica!
No trajeto de A a B, não há atrito então a energia mecânica do bloco em A, logo antes dele ser solto, é igual à sua energia mecânica chegando em B.
Nesse trecho não há nenhum mola atuando (o bloco não tem energia potencial elástica), então a energia mecânica é a soma da energia cinética com a energia potencial gravitacional:
Passo 2
Na posição A, o bloco:
- está no repouso, então sua energia cinética é nula: .
- está a uma altura , então sua energia potencial gravitacional é .
Na posição B, o bloco está no nível do chão, portanto sua energia potencial gravitacional é nula: . E queremos achar sua energia cinética !
Passo 3
Aplicando a conservação da energia mecânica:
Passo 4
Beleza, mas ainda falta achar trabalho realizado pela força da gravidade no trecho AB.
Mas isso também vai ser tranquilo: basta aplicar a regra do trabalho da força peso!
O bloco desceu uma altura , então o trabalho é:
Passo 5
b)
As únicas forças atuando no bloco no trecho BC são o peso, a normal e a força de atrito. As duas primeiras não realizam trabalho sobre o bloco por serem ortogonais ao sentido de deslocamento. Então o trabalho total realizado sobre o bloco nesse trecho é o trabalho da força de atrito!
E pelo teorema trabalho-energia cinética, o trabalho total é igual à diferença de energia cinética:
Portanto,
Passo 6
a gente já sabe que vale , mas ainda falta achar . Agora que vamos usar a informação que ele deu: “o bloco chega à posição C com metade da velocidade com que ele chegou em B”. Não precisamos nem calcular essas velocidades, o que nos importa são as energias cinéticas! e são dadas por
Substituindo :
Passo 7
Voltando a o que a gente tinha antes:
E como :
Passo 8
Ainda falta achar o coeficiente de atrito cinético. Podemos aproveitar o fato de já termos achado o trabalho da força de atrito!
Lembrando que a força de atrito é dada por
sendo o coeficiente de atrito cinético e o módulo da força normal.
Passo 9
O trecho BC tem comprimento , então essa é a distância que temos que considerar pra calcular o trabalho! E como a força de atrito é contrária ao sentido do movimento, o trabalho que ela realiza é negativo. Então temos
Como , isso dá:
E antes achamos
Comparando as duas expressões, concluímos que
Passo 10
c)
Agora queremos o trabalho realizado pela mola enquanto ela á comprimida.
Não adianta nada calcular o trabalho em função de já que não sabemos o valor de ; essa vai ser a segunda etapa da questão!
Então podemos proceder que nem na letra b), achando o trabalho a partir do teorema trabalho-energia cinética:
E agora que não tem mais atrito, a única força realizando trabalho sobre o bloco é a força elástica da mola! Ou seja:
sendo a energia cinética final do bloco e a energia cinética com qual ele chega pra comprimir a mola.
Passo 11
Repare que , porque depois de comprimir a mola o bloco para!
Ou seja,
Então só resta determinar com que energia cinética o bloco chega na mola!
Passo 12
Analisando friamente a situação, podemos ver que do ponto C até a mola não tem nada (atrito, mola, etc.)! As únicas forças atuando são o peso e a normal, se cancelando no eixo , mas não há nenhuma no eixo ! Então nesse trecho, o bloco está seguindo um MRU, ele tem velocidade constante.
Assumindo que o bloco não emagreceu do ponto C até a mola, a sua energia cinética ficou constante, pois ela só depende da massa e da velocidade do bloco! :)
Isso tudo pra dizer que . Ou seja,
Passo 13
Excelente! Então agora se a gente calcular o trabalho da mola pela forma convencional e comparar com o que acabamos de achar, vai dar pra achar !
O próprio enunciado dá a fórmula:
sendo o deslocamento inicial do bloco e seu deslocamento final quando ele atingir o repouso.
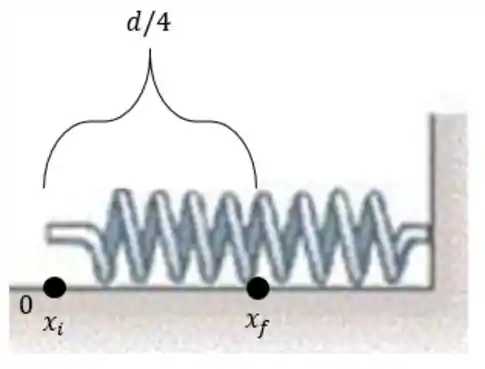
A gente sabe que o bloco comprime a mola de uma distância de : isso significa que . Assim, fixando o zero de deslocamento no começo da mola, temos e , dessa forma:
Passo 14
Então o trabalho realizado pela mola é:
Passo 15
E antes a gente achou:
Logo,
Show! :D
Passo 16
d)
Depois de ser comprimida pelo bloco, a mola empurra ele no outro sentido, realizando trabalho de novo. E esse trabalho é exatamente o mesmo da ida, só que com o sinal trocado! Pois é, não tem atrito, então tudo que a mola recebe ela devolve!
Se isso não te convenceu, dá uma olhada! Vamos considerar o trajeto do bloco desde o ponto em que ele começa a ser empurrado de volta pela mola até o ponto C.
Pelo teorema trabalho-energia cinética:
Ou seja,
Como o bloco parte do repouso, sua velocidade inicial é nula, então . Logo,
O trabalho é positivo porque a mola faz força no mesmo sentido do deslocamento!
Passo 17
O principal é que o bloco chega no ponto C com uma energia cinética , e ele ainda tem o trecho BC (que é onde tem atrito) pela frente.
Vamos tentar achar com que energia cinética o bloco chega no ponto B. A única força que realiza trabalho sobre o bloco é a força de atrito, então de novo temos
E pelo teorema trabalho-energia cinética (sério, a gente já usou ele tantas vezes nessa questão que eu te proíbo de esquecer ele na hora da prova haha):
Ou seja,
Passo 18
Sendo que lá atrás, nós já vimos que
A força de atrito é constante, é algo inerente ao solo, então o bloco pode atravessar o trecho quantas vezes quiser que o trabalho realizado vai ser sempre esse!
Enfim, isso vai dar
Opa! A energia cinética não pode dar negativo! Então deu ruim? Não! Isso simplesmente significa que o bloco não tem energia suficiente pra atravessar o trecho com atrito, pois .
Então o bloco vai parar ali na meiúca mesmo. Até daria pra calcular o quanto o bloco anda no trecho BC até parar, mas aqui só pedem pra achar que altura ele vai subir. No caso, como nem no ponto B ele chega, essa altura é zero!
Resposta
a)
b)
c)
d)