Considere o triângulo curvilíneo cujos lados são:
- O gráfico de para
- O segmento de reta que liga os pontos e
- E o arco de círculo de centro e raio , que tem
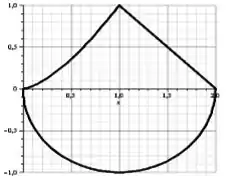
Escreva as três integrais que permitem calcular os comprimentos dos três lados do triângulo curvilíneo.
Determine o perímetro do triângulo curvilíneo.
Passo 1
Vamos aplicar a fórmula do comprimento de curva para os três lados:
A questão agora é só descobrir as funções correspondentes a cada curva e seus , ou seja, suas derivadas.
Passo 2
Para a primeira, já temos a função:
A derivada será
Logo, a integral, que fica entre , é:
Passo 3
Vamos descobrir a outra função que é a reta de até :
Então, essa reta é . Logo, é:
A integral fica assim, com indo de até :
Passo 4
A última função é a parte debaixo de uma circunferência, que tem essa equação:
Vamos isolar :
E aí, a equação será ou ? Repara que a gente está onde , então ficamos com a segunda opção. Derivando:
Jogando na equação, teremos isso (para indo de até ):
Passo 5
Vamos calcular a soma desses comprimentos, que vai dar o comprimento do triângulo:
Agora basta resolver cada uma das integrais
Passo 6
Começamos com a primeira:
Substituindo o termo da raiz por , temos:
Assim,
Passo 7
Fazemos a segunda integral agora:
Passo 8
A última integral:
Ela parece ser meio chatinha de ser resolvida assim, né? Mas o enunciado não nos pediu que resolvesse ela, e sim que achássemos o perímetro. Vamos usar uma malandragem!
Ué, ela não representa uma meia-circunferência? Sabemos calcular o perímetro de uma circunferência:
A metade disso, para , nos dará o resultado desejado:
Bem melhor do que resolver essa integral, né?
Passo 9
Assim, o perímetro do triângulo será: