A entrada de um dos estádios para as Olimpíadas de 2016 tem a forma da figura abaixo, e é constituída por 2 tubos circulares na forma de arco de curvas e , iluminados internamente com as cores dos países participantes. O custo estimado para estes tubos é de por metro. A curva é determinada por: e a curva por: . Determine o custo total desta obra.
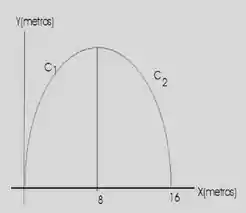
Passo 1
O problema pede o custo da obra. O custo é dado por metro, ou seja, para calcularmos o custo, precisamos saber o comprimento dos arcos. Logo, trata-se de um problema sobre comprimento de arcos. O enunciado nos deu as fórmulas e os limites de integração no desenho. Estamos com a faca e o queijo na mão. Vamos lá.
Passo 2
Esse problema tem um “pulo do gato”!
Não precisamos calcular o comprimento de E de . Olhe para as fórmulas:
e
Repare que a diferença é só a substituição de por . Isso acontece porque é espelhada. Portanto, os arcos são simétricos e possuem o mesmo comprimento.
Vamos calcular só o comprimento de e multiplicá-lo por . Depois, basta multiplicar pelo custo por metro para acharmos o custo total.
A fórmula para calcularmos o comprimento de um arco é:
Passo 3
Curva :
Essa integral parece ser muito difícil de ser calculada. Vamos tentar usar o método :
Fazendo a substituição
Aplicando:
Logo o custo total será:
Obs:
Nesse problema, tivemos que calcular em função de , já que facilitou muito o cálculo da integral. Portanto, se você estiver em um problema de comprimento de arco e cair em uma integral enrolada de calcular, tente fazer em relação a para ver se a situação melhora!
Resposta
O custo será de