Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Comprimento de Arco

Ver Teoria
Exercício 45123456789101112131415161718192021222324252627282930313233343536373839404142434446474849505152535455565758596061626364656667686970717273747576777879808182838485

Enunciado

IME, Cálculo 2, 2020, VE1, Q1b

Determine o comprimento das curvas abaixo:

  1. A parábola y = x 2 2 ;       0 ≤ x ≤ 1
  2. O cardioide r = 1 + s e n   θ ;       0 ≤ θ ≤ 2 π

Passo 1

Meus consagrados, lá vamos nós com comprimento de arco. É sempre bom ter uma ideia das curvas por isso pus abaixo os gráficos. O problema se trata basicamente de aplicar a integral de comprimento de arco para coordenadas polares ( r , θ ) . Sendo elas:

L = ∫ θ 1 θ 2 r 2 + d r d θ 2

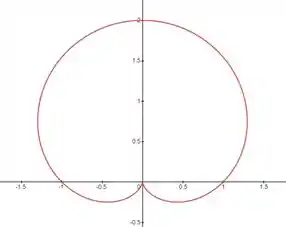
Passo 2

  1. Com r = 1 + s e n   θ , temos:

    2. L = ∫ 0 2 π r 2 + d r d θ 2   d θ = ∫ 0 2 π 1 + s e n   θ 2 + cos ⁡ θ 2   d θ

    L = ∫ 0 2 π 1 + 2   s e n   θ + s e n 2   θ + cos 2 ⁡ θ   d θ =   ∫ 0 2 π 2 + 2   s e n   θ   d θ

    L = ∫ - π   π 2 + 2   s e n   θ   d θ

    Uma vez que o integrando é periódico de período 2 π . Uma solução para integrais não-imediatas de funções trigonométricas é converter seno em função de tan ⁡ θ 2   através de:

    s e n   θ = 2 tan ⁡ θ 2 1 + tan 2 ⁡ θ 2

    De modo que, para - π ≤ θ ≤ π e - ∞ < u < ∞ :

    u = tan ⁡ θ 2 ⇒ d u = 1 2 sec 2 ⁡ θ 2 d θ ⇒ d θ = 2 d u 1 + u 2

    E assim:

    L = ∫ - ∞   ∞ 2 + 4 u 1 + u 2   2 d u 1 + u 2 = 2 2 ∫ - ∞   ∞ 1 + 2 u + u 2 1 + u 2   d u 1 + u 2

    L = 2 2 ∫ - ∞   ∞ 1 1 + u 2 3 / 2 + u 1 + u 2 3 / 2   d u  

    L = 2 2   ∫ -   π   π 1 1 + tan 2 ⁡ θ 2     3 / 2 1 2 sec 2 ⁡ θ 2 d θ   + 2 2   1   1 + u 2 1 2 - ∞ ∞

    L = 2 ∫ -   π   π 1 sec 2 ⁡ θ 2 3 / 2 sec 2 ⁡ θ 2 d θ + 0 = 2 ∫ -   π   π 1 sec 3 ⁡ θ 2 sec 2 ⁡ θ 2 d θ

    L = 2 ∫ -   π   π cos ⁡ θ 2 d θ = 2 2   s e n θ 2   - π π = 4 2

      L = 4 2

    Resposta

  2. L = 4 2

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Conforme a figura abaixo, uma viga horizontal com dimensões 2 pol × 6 pol × 16 pés (12 pol = 1 pé) fixada nos dois extremos é sujeita a uma carga uniformemente distribuída de 120 lb/pé. Como resultado
Encontre a função comprimento de arco para a curva y = ln ⁡ s e n x ,0xπ , com o ponto inicial π 2 , 0 .Trace a curva e faça o gráfico de sua função comprimento de arco na mesma tela.
Escreva, mas não calcule, uma integral para o comprimento da curva. x = y + y 3 , 1 ≤ x ≤ 4
Ache o comprimento da curva.y = ln ( sec x ) , 0 = x = pi // 4
Ache o comprimento da curva.y = 3 + (1)/(2) cosh 2 x , 0 = x = 1