Determine o comprimento das curvas abaixo:
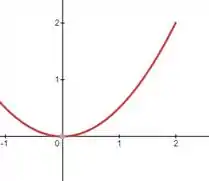
- A parábola
- O cardioide
Passo 1
Meus consagrados, lá vamos nós com comprimento de arco. É sempre bom ter uma ideia das curvas por isso pus abaixo os gráficos. O problema se trata basicamente de aplicar a integral de comprimento de arco para coordenadas retangulares ) sendo ela:
Passo 2
- Sabendo que:
A fórmula do comprimento de arco fica:
Agora, utilizaremos a substituição biunívoca:
com o respectivo intervalo de integração. Assim,
Para , , logo:
A qual resolveremos por integração por partes, definindo:
Assim,
onde passamos para o outro lado e dividimos por 2. Por fim, substituindo os valores: