Lista 2.10 – Derivada de ordem superior – UFSC – Cálculo 1 – Questão C2
Mostre que satisfaz a equação .
Passo 1
Falaee, beleza?? Seguinte.. vamos primeiro derivar a função que nos foi dada:
E, fazendo a segunda derivada, temos:
Passo 2
Agora, vamos substituir os valores encontrados em . Se liga aee:
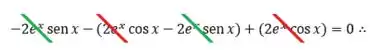
Logo, podemos confirmar que satisfaz a equação .
Entendeu direitinho? Responde aee ;)
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcule g^' (x) g (x) = ln x
Calcule g^' (x) g (x) = log_3 x
Calcule g^' (x) g (x) = log_pi x
Calcule f^' (x) .f (x) = pi^x
Calcule f^' (x) .f (x) = 2^x