UTFPR– Equações Diferenciais – AVA1 – Lista 4 – Questão 3c
Nos problemas de (a) até (c), resolva o problema de valor inicial
Passo 1
Oi, tudo bem por aí? Essa questão parece ser complicada, mas relaxa, vou fazer passo a passo com você! Bora lá? Precisamos resolver esse problema de valor inicial
Um dos termos é uma função que é definida por partes! E agora, como fazer?
A ideia aqui é resolver em duas partes: uma para cada etapa da . Iremos encontrar duas soluções: cada uma será válida no mesmo intervalo de validade da . Mas e qual é o mistério aqui?
Está justamente no valor inicial!
O valor inicial dado foi
Que abrange apenas a primeira parte da função, quando temos no intervalo de definição. Mas precisamos que a solução da segunda etapa também tenha uma condição inicial, e agora?
Isso mesmo! Essa vai ser a condição inicial da solução da segunda etapa da equação diferencial, quando usando a segunda parte da função !
Mas relaxa, vou fazer passo a passo com você! Vamos começar?
Passo 2
Nossa equação é essa aqui
E a função é definida por partes assim
Vamos começar resolvendo essa equação quando , válido quando :
Essa equação é do tipo
Onde !
A solução via fator integrante é essa aqui
O fator integrante é
Agora é só substituir na solução e integrar!
Assim temos
Do lado direito vamos resolver pelo método de integração por partes
Beleza?
Agora se você não lembra como escolher , aqui vai um refresco
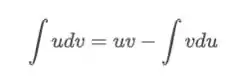
Assim temos que , e , aplicando por partes na direita temos
Beleza até aqui?
Temos
Aí nossa solução para é
Estamos quase lá! Vamos para a segunda etapa de ?
Passo 3
Agora antes de seguir resolvendo a segunda parte, precisamos encontrar qual é a condição inicial dessa segunda etapa!
Sabemos que a solução até é essa aqui
Encontrada no passo anterior, então o valor que a solução assume no final do intervalo é o valor inicial da segunda solução!
Beleza? Agora vamos resolver essa segunda equação diferencial, e no final aplicar essa condição inicial!
Nossa função é
E assim a equação diferencial fica
Vamos usar o mesmo método: fator integrante! Mas agora e .
E a nossa solução
Assim a solução dessa segunda parte fica assim
E por fim, vamos descobrir qual é essa segunda constante! Temos a condição inicial (dessa etapa)
E aplicando na solução temos
E nossa solução particular para fica assim
Ufa! Agora sim terminamos! A ideia de usar uma função definida por partes em uma equação diferencial é essa: no extremo final de um intervalo vamos encontrar a condição inicial do próximo. Caso a fosse divida em mais uma etapa, estaríamos agora encontrando a condição inicial associada a esse próximo intervalo
Recapitulando nossas respostas! A solução é
E é isso! Terminamos! Vamos treinar mais?