Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de EDO Linear de 1ª Ordem

Ver Teoria
Exercício 481234567891011121314151617181920212223242526272829303132333435363738394041424344454647495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFMG, Sem Campus, Equações Diferenciais A, Listas de EDA - Profª Alejandra Russi - Lista 2 - Equações lineares, Bernoulli e separáveis, Questão 3.2

Resolva os problemas de valor inicial abaixo, indique o intervalo de validade da solução encontrada e esboce seu gráfico:

y y ' + y 3 = 1

y ( 0 ) = 1

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de EDO. Nosso objetivo é Resolver o problema de valor inicial

y y ' + y 3 = 1

y ( 0 ) = 1

Indicando o intervalo de validade da solução encontrada e esboçar seu gráfico.

Passo 2

Vamos resolver

y y ' + y 3 = 1

y ( 0 ) = 1

Escrevendo y ' = d y d t

y y ' + y 3 = 1

⇒ y d y d t + y 3 = 1

isolando o d t

⇒ y 1 - y 3 d y = d t

Integrando, temos:

∫ y 1 - y 3 d y = t + c

fazendo

y 3 / 2 = u

⇒ 3 2 y 1 / 2 d t = d u

Então, a integral fica

2 3 ∫ d u 1 - u = t + c

⇒ - 2 3 l o g ( 1 - u ) = t + c

Logo

- l o g ( 1 - y 3 / 2 ) = 3 2 ( t + c )

⇒ y = ( - e - 2 3 ( t + c ) + 1 ) 2 / 3

Encontramos a solução para nossa EDO

Passo 3

Vamos resolver o problema de valor inicial:

Temos que

y ( 0 ) = 1

Logo, como

y ( t ) = ( - e - 2 3 ( t + c ) + 1 ) 2 / 3

⇒ 1 = ( - e - 2 3 ( c ) + 1 ) 2 / 3

⇒ c = - 3 2 l n ( 2 )

Essa solução é válida para todo R

E temos o esboço da nossa solução:

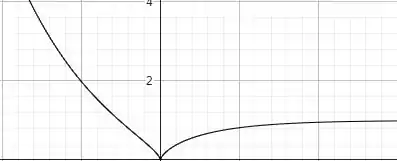
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento acima

Exercícios de Livros Relacionados

Resolva a equação diferencial.y^' = (e^y)/(x y)
Resolva a equação diferencial:y^' = x e^(x - y) c o s s e c y
Resolva o problema de valor inicial.t (d u)/(d t) = t^2 + 3 u , t0 , u (2) = 4
Determine se a equação diferencial é linear.x y + sqrt(x) = e^x y '
Determine se a equação diferencial é linear.x y^' + ln x - x^2 y = 0