UTFPR– Equações Diferenciais – AVA1 – Lista 4 – Questão 2c
Nos problemas de (a) até (c), resolva o problema de valor inicial. Dê o maior intervalo sobre o qual cada solução está definida
Passo 1
Oi pessoal, tudo bem por aí? Vou te ajudar nessa questão! Bora! Precisamos resolver essa equação diferencial ordinária aqui
Você tasca o olho nessa equação e percebe que ela pode ser escrita como
E aí você logo lembra: Fator integrante! E é isso mesmo!
São duas as pistas que te ajudam a identificar que vamos usar esse método:
- é que tem um ali dando sopa!
- Todos os coeficientes ou são constantes, ou dependem apenas de !
Mas além de achar a solução geral, você vai precisar achar a particular! Foi dado um valor inicial
Não esqueça de encontrar o valor da constante ok?
Depois de achar a solução ainda precisamos ver o maior intervalo em que ela é válida! Lembrando que aqui você precisa tirar do intervalo valores de que deixam a solução inválida, tipo divisão por zero, logaritmo de número negativo, essas coisas
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Já descobrimos qual o método que vamos usar, agora é #partiusolução
No método de fator integrante, nós vamos chamar esse fator de e considerando que nossa edo está escrita assim
Nosso fator integrante é
Nossa edo é
Vamos começar trocando por e dividindo tudo por
Pronto! Nossa edo já está no formato que queremos! Temos que
E o nosso fator integrante fica assim
Para essa integral vamos chamar
Aí temos
E agora voltando para
Tudo bem até aqui?
Assim nosso fator integrante é
Obs.: Até aqui temos uma restrição para o . Nosso fator integrante veio de um logaritmo, certo? Então precisamos garantir que o argumento desse logaritmo seja positivo, assim
Você pode encontrar em outras questões, e aí precisa ir anotando tudo que o não pode ser, ok?
Passo 3
Agora que calculamos nosso fator integrante, vamos para a solução! Sendo a equação diferencial assim
Por isso que precisávamos encontrar antes o fator integrante! Vamos recapitular! Nossa edo
Aí temos
E o fator integrante
Agora é substituir na solução !
Agora basta resolver!
Mas como resolver essa integral do lado direito?
Essa integral era resolvida pelo método de integração por partes, lá do cálculo, naqueles tempos longínquos. Você lembra como escolher e ? Através desse esquema aqui, saca só:
Assim temos que
Aplicando por partes
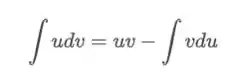na nossa integral
Tudo bem até aqui?
Aí nossa solução fica assim
Beleza?
Ufa! Estamos quase lá!
Passo 4
Nosso próximo passo é determinar quem é aquela constante na solução: e isso vamos fazer através do valor inicial
Na nossa solução
Oba! Encontramos nossa solução particular
E o intervalo de validade? Como dividimos pela função lá no começo, e esse termo era argumento de um logaritmo, precisamos garantir que e , e isso ocorre no maior intervalo entre
E é isso! Acabou a questão! Vamos para a próxima?