Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética de Rotação

Ver Teoria
Exercício 181234567891011121314151617192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899

Enunciado

UnB – Física 1- Listas – Lista 12: Dinâmica do Movimento – Questão 8a

Um alvo é constituído por uma placa quadrada de madeira vertical com lado igual a 0,250   m   e massa de 0,750   k g , pivotada em um eixo horizontal situado em seu topo. A placa é atingida frontalmente em seu centro por uma bala de massa igual a 1,90   g   que se desloca a 360   m / s   e que fica retida no interior da placa.

a) Qual é a velocidade angular da placa logo após o impacto da bala?

Passo 1

Falaaa, gente linda! Tudo certo com vocês? Essa questão parece complicadinha, eu sei… 

Sai pra lá gatinho, quero você aqui feliz e animado, igual nossos alunos do Responde Aí. Assim, olha:

Então temos uma placa presa por um pivô que é atingida por uma bala. A nossa missão consiste em encontrar qual será a velocidade angular da placa após essa colisão. Como faremos isso??

Como não há forças externas e nem torque externo, podemos afirmar que os momentos angulares e lineares se conservam. Assim, como estamos interessados em descobrir a velocidade angular, é ideal utilizarmos a conservação do momento angular antes e depois da colisão.

A representação do problema pode ser dada por:

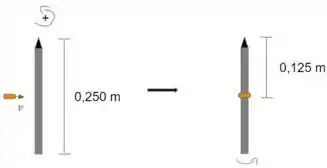
Sabendo disso, vamos calcular o momento angular inicial. No instante inicial a bala ainda não está retida na placa. Então para o momento angular inicial vamos utilizar a fórmula:

L i = m v r

Onde,

m : m a s s a   d a   b a l a ;

v : v e l o c i d a d e   d a   b a l a ;

r : r a i o   ( t a m a n h o   d o   e i x o   d e   r o t a ç ã o ) ;

Como pouco antes da bala atingir a placa, essa se encontrava a uma distância de l 2 da borda da placa. Podemos afirmar que esse será o tamanho do nosso eixo de rotação.

Logo, a nossa fórmula para calcular o momento angular inicial terá essa carinha:

L i = m v l 2

Substituindo os valores correspondentes. Temos que:

L i = 1,9 ⋅ 10 - 3 k g 360 m s 0,250   m 2

L i = 0,0855   k g ⋅ m 2 / s

Passo 2

Galerinhaaa, agora precisamos calcular o momento angular final. Lembrando que agora a placa quadrada estará girando juntamente com a bala. Humm... pensando nisso, como poderemos encontrar esse momento angular final??

Deixa que eu te ajudo! Vamos utilizar a seguinte fórmula:

L f = I f w f

Onde,

I f : m o m e n t o   d e   i n é r c i a   f i n a l ;

w f : v e l o c i d a d e   a n g u l a r   f i n a l ;

Como a bala estará presa dentro da placa, o momento de inércia será dado pelo momento de inércia da placa juntamente com o momento de inércia da bala.

I f = I p l a c a + I b a l a

Pelo teorema dos eixos paralelos o momento de inércia da placa ( I p l a c a ) será dado por:

I p l a c a = I c m + M d ²

Sendo d a distância até o novo eixo, isso significa que é a distância entre o pivô que segura a placa e o local em que a bala atinge a placa.

I p l a c a = I c m + M ( l 2 ) ²

I p l a c a = M l 2 12 + M ( l 2 ) ²

Logo,

I p l a c a = 1 3   M l ²

Lembrando que M representa a massa da placa.

E como a bala é uma partícula, o momento de inércia de partículas é dado por:

I b a l a = m r ²

Portanto, o momento de inércia final será:

I f = I p l a c a + I b a l a

I f = 1 3 M L 2 + m r ²

Substituindo com os valores correspondentes, encontramos que:

I f = 1 3 0,75   k g 0,25   m 2 + 1,9 ⋅ 10 - 3 k g ( 0,125   m ) ²

I f = 0,01565   k g ⋅ m ²

Podemos concluir então que o momento angular final será:

L f = I f w f

L f = ( 0,01565   k g ⋅ m 2 ) w f

Passo 3

Ufaaa...

Por fim, como há conservação do momento angular. Vamos igualar o momento angular inicial com o momento angular final.

L i = L f

0,0855   k g ⋅ m 2 s = 0,01565   k g ⋅ m 2 ω f

E assim, descobrimos que a velocidade angular logo após o impacto da bala é

  ω f = 5,46   r a d / s

Show??! Essa realmente foi complicadinha porque envolveu um monte de outras fórmulas. Mas, eu garanto que com o treino de mais questões desse estilo na hora da prova você tira de letra 😉

Resposta

ω = 5,46   r a d / s

Exercícios de Livros Relacionados

Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremi
Na figura abaixo, uma barra fina e homogênea (com 4 m de comprimento e uma massa de 3 k g ) gira livremente em torno de um eixo horizontal A que é perpendicular à barra e passa por um ponto situado a
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezíve
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que