Sejam duas massas e penduradas por um fio inextensível de massa desprezível a uma polia ilustrada na figura. A polia consiste um anel de massa e raio e hastes de massa . Veja a figura.
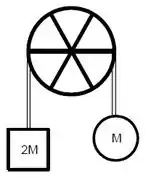
O momento de inércia rotacional da polia em relação ao seu eixo é . O sistema é solto do repouso e o atrito é desprezível.
Determine a variação da energia potencial gravitacional do sistema desde o instante em que foi solto até o instante em que o módulo da velocidade das massas for igual a .
Passo 1
Uma dica inicial: Não se desespere com detalhes estranhos (tipo essa polia bizarra). Leu a questão toda? Consegue imaginar a forma que você costuma resolver algo assim? Então vá em frente, e quando surgirem os detalhes estranhos, você pensa neles.
Dito isso, vamos começar a questão.
Como ele quer a variação da energia potencial gravitacional, esse é um problema de energia, e não vamos gastar tempo desenhando as forças do sistema. A conservação da energia diz que:
Onde é a energia potencial do sistema e é a energia cinética do sistema (tanto linear quanto rotacional).
Rearrumando, temos:
Como o sistema parte do repouss, temos então que:
Passo 2
Agora vamos achar a energia cinética final do sistema.
Como as massas estão unidas por um fio inextensível, então teremos que o módulo das velocidades vão ser iguais.
Pois elas vão sempre percorrer mesma distância em um mesmo tempo.
A energia cinética devido a essas massas então vai ser:
Agora, temos a energia cinética de rotação da polia estranha, dada por:
Pela cinemática do problema, temos:
E assim:
De acordo com o problema, o momento de inércia da polia é . Quando ele diz isso, ele quer dizer do anel junto com as hastes! Então é só substituir:
O que dá que a energia cinética final do sistema vai ser:
Logo:
Observação: Nota que o enunciado diferencia quem ele chama de “polia” (anel + hastes) e quem ele chama de “anel”, já dando direto o momento de inércia da polia toda. Então não se preocupe em calcular ele, já que o problema já te dá ele direto!
Se você fosse de fato calcular o momento de inércia da polia, precisaria somar o do anel e das três hastes.
Sendo que o tamanho de cada haste é um diâmetro do anel. Assim:
De fato, o momento de inércia dado na questão.