Um disco e um anel de mesmo raio, mesma massa total e mesma velocidade, rolam sem deslizar sobre uma superfície plana. Em um dado momento, ambos encontram um plano inclinado e o sobem até pararem momentaneamente. Qual a razão entre a altura máxima atingida pelo anel pela altura máxima atingida pelo disco? Formulário: ,
A.
B.
C.
D.
E.
Passo 1
Vamos desenhar o que ele tá falando:
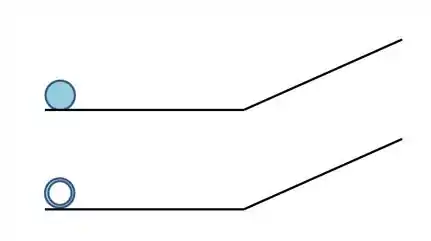
A gente tem esses dois corpos rolando sem deslizar, aí eles vão subir o plano inclinada até um ponto e vão para. Então, nós queremos a razão dessas alturas máximas.
Vamos lá.
Passo 2
Ele não fala nada sobre atrito, então considerando que não temos atrito, temos que a energia mecânica se conserva, isto é: a energia do corpo quando está no plano (temos somente energia cinética, de rotação e translação) rolando sem deslizaré igual a energia de quando o corpo chega ao ponto mais alto do plano inclinado(só tem energia potencial).
Isolando a altura máxima:
Passo 3
Então, para o disco.
Sabemos que
Como rola sem deslizar:
Então:
Resolvendo isso daí:
Maravilha!
Passo 4
Para o anel.
Sabemos que
Como rola sem deslizar:
Então:
Resolvendo:
Passo 5
Calculando a razão:
Resposta
Alternativa E