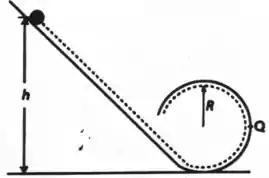
Uma bola de gude de massa e raio rola sem deslizar ao longo do trilho curvo mostrado na figura, tendo sido abandonada do repouso em algum lugar sobre a parte reta do trilho. A linha pontilhada descreve a trajetória do centro de massa da bola de gude.
Dado: Momento de inércia de uma esfera girando ao redor do eixo que passa pelo seu centro de massa:
- Desenha as forças que agem sobre a esfera quando ela desce a parte reta do trilho, justificando o sentido da força de atrito.
- De que altura mínima acima da base do trilho se deve abandonar a bola a fim de que ela se mantenha no trilho no topo da circunferência?
- Se a bola é abandonada de uma altura acima da base do trilho, qual será o módulo da componente horizontal da força atuante sobre ela no ponto
Passo 1
a):
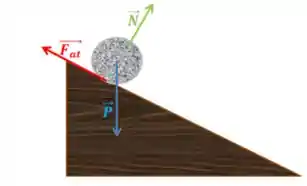
Onde:
Normal.
Peso.
: Força de atrito.
A força de atrito tem esse sentido porque deve fazer a esfera girar no sentido horário, já que ela está descendo o plano.
Passo 2
b):
Bom, nesse tipo de pergunta, a gente tem que primeiro analisar as condições que a bolinha adquire quando chega lá em cima da volta.
Lá em cima, a normal será nula. Então, lembrando também que a força resultante é a força centrípeta, vamos ter:
Então é essa a velocidade que a esfera precisa ter quando atingir o topo da volta.
Passo 3
Agora vamos pra conservação de energia. Como a energia mecânica se conserva, a energia potencial do inicio vai ser a mesma que a energia mecânica lá no topo da volta.
Bom, a energia mecânica inicial é toda potencial e vale:
E a final:
Lembrando que a altura final é Além disso, pela condição de rolamento sem deslizamento:
Então:
Usando:
Então:
Ufa! Simplificando isso ae:
Beleza? Só tem tomar cuidado com todas essas contas bestas ai. Agora, comparando com a energia mecânica inicial:
Passo 4
c):
A charada aqui está em achar a velocidade que a bola vai ter quando atingir essa posição. Ai você usa:
Afinal de contas, na direção horizontal só vai ter atuação da força centrípeta, que será igual a normal:
Assim, usando a conservação de energia mais uma vez:
Usando:
Então:
Ai que tá. A gente pode manipular esse troço pra conseguir a expressão da força centrípeta assim:
Resposta
a):
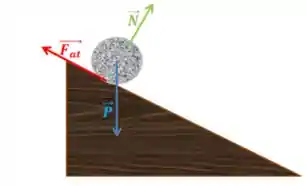
b):
c):