Duas polias com massas e estão acopladas através de uma correia de massa desprezível, como mostra a figura ao lado. A polia é acelerada a partir do repouso com aceleração angular durante o tempo .
As polias têm raios e , respectivamente, e podem girar sem atrito.
O momento de inércia de uma polia é dado por .
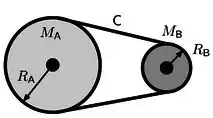
- Calcule as velocidades angulares das polias e no instante de tempo
- Obtenha a fração entre as energias cinéticas das polias e , no instante de tempo .
Passo 1
Na polia temos que a velocidade angular em função do tempo é dada por
Como as polias são aceleradas a partir do repouso temos que . Assim no instante
Passo 2
Como a correia não desliza, temos que a velocidade linear nas bordas das polias é igual, ou seja
E podemos relacionar essas velocidades lineares com as velocidades angulares por .
Assim
Passo 3
A energia cinética de rotação é dada por
De modo que a razão fica
Resposta
(A) e
(B)
Exercícios de Livros Relacionados
Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremi
Na figura abaixo, uma barra fina e homogênea (com 4 m de comprimento e uma massa de 3 k g ) gira livremente em torno de um eixo horizontal A que é perpendicular à barra e passa por um ponto situado a
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezíve
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que